The Chemistry of Platonic Triangles:
Problems in the Interpretation of the Timaeus
D. Robert Lloyd*
Abstract: Plato’s geometrical theory
of what we now call chemistry, set out in the Timaeus, uses
triangles, his stoicheia,
as the fundamental units with which he constructs his four elements. A
paper claiming that these triangles can be divided indefinitely is
criticized; the claim of an error here in the commentary by F.M.
Cornford is unfounded. Plato’s constructions of the elements are
analyzed using simple point group theory. His procedure generates fully
symmetric polyhedra, but Cornford’s ‘simpler’ alternatives generate
polyhedra with low symmetries and multiple isomeric forms. However,
Cornford’s principle of constructing larger triangles by assembling
smaller ones is still valid.
Keywords: Plato’s chemistry,
elements, F. M. Cornford, group theory, Platonic solids.
Introduction
The Timaeus[1]has
been the object of study and commentary ever since its appearance,[2]
and was long regarded as the most significant work of Plato. As an
indication of this importance through the late middle ages and beyond,
Raphael (1483-1520), in his fresco ‘The School of Athens’,
characterizes Plato by showing him holding this work in his hand
(apparently written in Italian!). In his extraordinary work, Plato sets
out to provide a "reasonable account" (eikos logos) of the whole
of Creation by the ‘Demiurge’, both at the cosmic scale and also at the
microscopic level. It is important to appreciate, given the intervening
Christian centuries, that neither is this is a creatio ex nihilo, nor
is the Demiurge omnipotent. Some versions in English give him the
literally translated name of ‘The Craftsman’; he works with the
pre-existing materials available to him, and I will return to this
point.
In the context of this Journal, Plato’s
account of
the nature of the four elements is his most significant contribution.
In the second part of the Timaeus, Plato sets out a scheme for
what we now call chemistry, biochemistry, and human biology. Concerning
this part, the view of Böhme and Böhme (1996, p. 100) is that
Timaeus
ist philosophie- und
wissenschaftsgeschichtlich von
außerordentlicher Bedeutung, weil er fast der einzige Text ist,
der von
den Dialogen Platons durchgängig in Europa den Gelehrten bekannt
war.
Dann aber insbesondere, weil er eine der Quellen war, aus denen sich
zur Zeit des alexandrinischen Neuplatonismus die Alchemie entwickelte.
Als solchen kamen die antiken Lehren von der Materie, vermittelt
über
die Araber, ins lateinische Mittelalter. Auf dem Hintergrund der
Alchemie entwickelte sich vom 17. Jahrhundert an die neuzeitliche
Chemie.
Thus, in their opinion, the dialogue counts as
one of the foundations of our modern chemistry, via
its influence on early alchemy. An understanding of chemistry as Plato
saw it is thus of some significance. The general outlines are clear.
His theory is partly based on the earlier four elements,[3]
but there are two very important additions to previous theories. The
first of these is that each of the traditional elements is to be
associated with the form of one of the regular polyhedra, which we
still call the Platonic Solids. He assigns the dodecahedron to the
entire cosmos, and the other four as elements. These four are
constructed using his truly elementary units, the stoicheia,
two particular right triangles. Chemistry, as he understands it, is
based on the most advanced mathematics available to him, geometry.
There are obvious parallels with our modern situation, in which quantum
mechanics, at some level or other, is fundamental to our understanding
of the subject.
The second addition, particularly relevant to
the
first part of this paper, is that each polyhedral form is the prototype
for a whole range of elements, where differently sized units have
notably different properties. For example the general class of elements
which he calls "fire" is associated with the regular tetrahedron.
Depending on the size of the tetrahedron, this can be conventional
fire, visible light (Tim. 58C) of various colors (67D), or it can be a
sort of radiation believed to be emitted from the eye as part of the
process of vision (45B-C). Similarly ordinary water and gold are both
considered "waters", associated with icosahedra: various forms of "air"
are all to be associated with different sizes of octahedra. (For a
summary of the differently sized elements, see Brisson and Meyerstein
1995, pp. 53-4, and Brisson 2003, pp. 15-16.)
These three different polyhedra are
considered to
be formed by assembling equilateral triangles. These triangles in turn
are made up by assembling six of what Plato considers truly elemental
units, stoicheia, scalene triangles with angles of 30º,
60º,
and 90º. (The construction is illustrated in Figure 1b). It is
very
important for Plato that because of these common triangular units, his
elements can interconvert (54C-D), unlike those of the atomic theories
of the time. He has problems with the fourth element type, earth,
because he has to assign this to the cube, which, being made up of
right-angled isosceles triangles forming squares, cannot interconvert
with the other three. Thus, within the Timaeus theory, there
are two shapes of elemental triangles, and each of these exists in more
than one size.
A particularly significant commentary on the
text of the Timaeus is F.M. Cornford’s Plato’s Cosmology
(1937), which, despite its age, is still probably the pre-eminent work
in the English language.[4]
This paper is concerned with two particular aspects of Cornford’s
analysis of the way in which Plato constructs the three-dimensional
regular units which make up the elements. Cornford did not accept that
Plato’s specified geometrical construction of the equilateral triangle
from six stoicheia was unique; rather it was to be understood
as a ‘sample’ of many different constructions using varying numbers of stoicheia.
In the second half of this paper I show that Plato’s specified
construction has to be taken more seriously; it is in fact the only way
to construct three-dimensional units with the true symmetry of the
regular bodies. Nevertheless, Cornford’s ‘building block’ approach, if
used with a proper consideration of symmetry, is still consistent with
Plato’s specification, even though some of his proposed structures have
low symmetry, and therefore have to be discarded.
In the earlier part of this paper, I deal
with a
related problem. Cornford’s proposal is that Plato’s differently sized
equilateral triangles should be considered as all made up by assembling
different numbers of the same size of elementary scalene triangle. This
has had wide acceptance, at least among writers in English.[5]
However, an earlier paper in this Journal, ‘A Potential Infinity of
Triangle Types: On the Chemistry of Plato’s Timaeus’,
by J. Visintainer, makes some remarkable claims concerning this point
in Cornford’s commentary. The abstract of this work begins (Visintainer
1998, p. 117):
Francis Cornford’s assertion that there must
be a smallest elemental triangle in the Platonic chemistry of the Timaeus
is overturned in this paper.
Visintainer’s proposal implies that Cornford’s
scheme of building up larger triangles from the same basic unit is
unnecessary – instead, differently sized scalene triangles can be
generated by subdivision of larger ones. Thus there need be no smallest
elemental triangle; any particular one can be indefinitely subdivided,
giving his "potential infinity" of triangles. On a variety of grounds,
I contend that this is not the case, and these arguments form the
subject of the first half of my paper.
Part I. Finite or Infinitesimal Triangles?
1. Triangles in the commentary by Cornford
The quotation above implies that Cornford made
a
specific new proposal "that there must be a smallest elemental
triangle". Reading his text, it seems likely that he would have been
surprised by the accusation. In fact he is discussing the construction
of larger triangles, and his geometrical proof that there is an
upward-going series of these is most easily shown with the device of a
downward-going argument of subdividing triangles. He may have been a
little careless in speaking of ‘Plato’ not continuing a process of
division, since there is no mention of any such division in the Timaeus
text here; this division is Cornford’s own.[6]
However, a similar criticism can be leveled at the statement
(Visintainer 1998, p. 123) "Plato never explicitly states that the
process of division of equilateral triangles does not continue
indefinitely." Since Plato has not discussed such division, there is no
obvious reason why he should.
2. Infinitesimals?
It is certainly clear that Cornford believes
the elementary triangles, Plato’s stoicheia,
to be finite, and not capable of being divided, but this was hardly a
new proposal of his. In the commentary by Taylor (1928, pp. 372-3),
published a decade earlier, there is a much more definite statement of
the point. "It is assumed [by Timaeus] that the faces of the
molecules can only be physically broken up along the lines of cleavage
which are the sides of ‘elementary’ triangles. The two ‘elementary’
triangles are physically the ultimates of the theory, and therefore
indivisibles, though they have finite areas, are not ‘infinitesimals’."
If there is to be a discussion of divisibility, and infinitesimals,
potential or otherwise, it is this text rather than Cornford’s which
should be considered.
Going further back, there is evidence from
Aristotle, who had been Plato’s student, that Plato intended the
triangles to be indivisible. According to Vlastos (1975, p. 67),
"Aristotle takes it for granted that Plato’s theory is a variant of the
atomic hypothesis of Leucippus and Democritus", commenting that "both
[theories] uphold ‘indivisible magnitudes’". There is a discussion of
this point in the Timaeus by Sorabji (1983), who states that
"Plato distinguishes between perceptible, mathematical and ideal
entities", and that although he does accept the possibility of infinite
divisibility, this is only for the latter entities, not for real,
"perceptible" ones. Concerning the triangles, the "elementary particles
are all rectilinear and, we may add, do not fall below a certain size."
More recently Gregory (2000, p. 203) has stated that "The evidence of
Aristotle then is very much in favor of the idea that the stoicheic
triangles do not undergo any sort of alloiôsis". Neither
of the
comments by Vlastos and Sorabji seems to have been taken into account
by Visintainer; the work proceeds to a demonstration that Plato could
have used a scheme of division leading to infinitesimal (or
"potentially infinitesimal") triangles in his scheme, but serious
questions remain. Firstly, bearing in mind the remarks above, would
Plato have had any interest in using such a procedure for a description
of the real world? Secondly, did he have any need for it? I turn to
this question now.
3. Triangles and mixtures, elements and compounds
The work includes the statement "I will
examine why
[…] the triangles are not given any definite size by Plato"
(Visintainer 1998, p. 117). Perhaps the most obvious reason is that
Plato did not need to, since so long as the largest unit is below the
level of visibility, any finite scale will do; indeed it is not even
clear how he could have made such an assignment of microscopic sizes.
However the main motivation for this work appears to be indicated by
the multiple references in the paper to the supposed ‘call’ of Plato
for an ‘endless diversity’ of elemental triangles. The basis for this
claim is the following footnote (Visintainer 1998, p. 128, note 4):
The Greek at 57d reads "tên poikilian
estin apeira’’. ‘poikilian’ refers there to the many
different or motley units from which the solids are ultimately made, i.e.
the triangles, be they of the right scalene type or the half square
type. These units are (estin) without limit (apeira).
The translations of the words (from 57D 4-5)
are
correct, but the deduction about triangles is not. An important
preceding clause has been omitted, and ‘poikilian’ does not
refer to triangles. Cornford’s translation of this part of the text has
"Hence, when they are mixed with themselves or with one another, there
is an endless diversity". Here ‘they’ refers to triangles and to the
"uncompounded and primary bodies" (akrata kai prôta
sômata, see the previous sentence) which they make up, but
the variety is of mixtures,
not of triangles or bodies. The "endless diversity" refers not to the
triangles at all, but to the complex mixtures possible with the many
different elements. In addition to the translation, on p. 230, Cornford
also makes this point clearly and quite specifically on p. 231, and
again in his notes introducing the next section (p. 246). On this
interpretation[7]
there is clearly no requirement
for an ‘endless diversity’ or ‘infinite variety’ of triangles. Not only
has Plato not "called for" this; he has not even suggested it.
In modern terms, it is perfectly possible to
state
that our ninety or so reactive elements can give rise to an "endless
diversity" of compounds. Indeed, given the non-stoicheiometric nature
of the phases, this is true just for iron and oxygen, and many other
pairs. Plato has not specified anything about the stoicheiometry of his
‘mixtures’, and in the phrase "tên poikilian estin apeira",
he is saying no more than that there is no limit to the number of
possible combinations of his elements.
Although the quoted phrase carries no
information
about the triangles/ primary bodies, the previous rather long sentence
does. We are told that there are "numerically as many as there are
varieties within a given form".[8]
Presumably Plato does not know how many species there might be, but
there is no suggestion that these numbers might be infinite; the
examples he gives suggest that, far from there being an ‘endless
diversity’, the actual numbers of elements, and of corresponding
triangles, would probably be rather small (Brisson and Meyerstein 1995,
pp. 53-4).
4. Can the atom be split?
The proposal (see Figures 9 and 10 of
Visintainer
1998, and the related text) is that if a structure such as an
equilateral triangle exists, it can be sub-divided indefinitely, taking
no account of the way in which Plato specified that it be constructed
from elementary scalene triangles, even though Plato considers
the function of these triangles to be similar to that of letters making
up syllables (47C). Indeed, Plato’s use of the word stoicheion,
originally ‘letter’, makes it immediately apparent that there is a
serious problem here. At 47B-C, he has rejected earlier atomic schemes
precisely because they have not come up with a truly fundamental unit,
a
‘letter’ of the alphabet, while he has (Zeyl 2000, p. 37, notes 50,
51). Using Plato’s metaphor, it is doubtful whether any significance
could be attached to a fraction of a letter, and certainly none could
apply if it were to be divided indefinitely.
We also need to consider the Demiurge and his
limitations. The triangles are a part of his working material. Using
them, he forms them into the elements which are then as nearly perfect
as possible (53B). The source of the triangles is not specified, but
whether they are a part of the initial chaotic ‘stuff’ of the cosmos
before he sets it in order, or he is making them as a part of creation
following the perfect model (28A-B), some of them are of higher quality
than others. Accordingly he has to carry out a special selection of the
best ones in order to form ‘marrow’ (73B). Thus once the creation is
over, the elementary triangles are fixed. If even the Demiurge has to
select, rather than remaking or smoothing off, no later process is
going to disturb them. However, Visintainer’s continuous division
demands a very severe disturbance indeed.
It is claimed that this work is following an
interpretation by Bruins (1951); specifically, in the above dissection
of elementary triangles it is stated that (Visintainer 1998, p.
122):
Then, following the scheme of Bruins (1951),
we
could see how, for any given equilateral triangle, it could become
itself a tetrahedron, given that it should ‘cut itself’ in the correct
way and ‘fold out’ into the third dimension (Fig. 10).
This misrepresents Bruins in several ways.
Nowhere
does he or Plato mention any unit ‘cutting itself’. What is discussed
at this point is the exact inverse of what is claimed, an unfolding
(rabattement/développment) of a tetrahedron, which has
been cut along edges,
into a four-fold equilateral triangle. The important point here is that
Bruins everywhere assumes that his equilateral triangles or squares are
made up of smaller units, scalene or isosceles, which are a-tomon,
and in this he is in agreement with the above quotation from Taylor
(1928). It is inconceivable that he would countenance a folding across
the elementary units as is shown by Visintainer in his Figures 9 and
10. Later, where Bruins demonstrates a division of a cube, he refers to
the cutting of the other polyhedra "along the edges of the
right-angled triangles",[9]
again echoing Taylor. For the cube, he makes it equally clear in his
diagram that the cutting is happening along the edges of pre-existing
isosceles triangles, and he uses this as a reason to argue in favor of
the Timaeus construction of the square. Some of his planar
units do indeed fold up during interconversions, but only along
pre-existing join lines. It is very clear that his implicit model for
the way in which larger units have been constructed follows, in
principle if not in detail, that of Cornford, the very model which
Visintainer claims is being overturned. For Bruins, in dividing
down or in folding, there will be a clear limit when the edges of the
elemental triangles are reached. The procedure described, which cuts or
folds across these, is in no way ‘following’ Bruins.
A related point against the idea of continued
division is that there are serious questions about how it could work.
It seems to need a supernatural agency, such as the Demiurge
continually interfering in his creation, and the evidence in the text
is in the opposite direction: after the creation, he withdraws from it
("he proceeded to abide at rest in his own customary nature", 42E).
Without this, it is difficult to see a mechanism for the process of
"cutting", which will need to be very precise if it is to produce
"matched sets" of smaller triangles suitable to build Plato’s regular
solids. Since Plato speaks of "battles" between particles of his
elements (81C-D, 56B), and is clearly thinking of violent impacts,
presumably random, we might expect random fragmentation rather than
precise cutting. If there are pre-existing cleavage lines, then there
must be smaller finite sub-units present, beyond which no further
cutting can take place.
Finally, there is an argument from Cornford
which is relevant. At 57C9 the phrase "tôn stoicheiôn
aitiateon sustasin" occurs. Although sustasis
can have the passive meaning of structure, Cornford comments that an
active meaning, of putting together, is the only possible meaning for
the text. His translation reads "The reason why there are several
varieties within their kinds lies in the construction of each of the
two elements". The ‘kinds’ refer back to the ‘uncompounded and primary
bodies’. Thus different sizes arise from different
assemblies/constructions; this is alluded to briefly in the second part
of this paper. However, in Visintainer’s scheme involving continuous
divisibility, there would be no reason to have such a difference of
assembly. The process of ‘putting together’ would be the same for any
size of triangle, so that this part of the Timaeus text would
be at least redundant, if not meaningless. Thus Cornford’s ‘building
block’ approach can still stand, and I now turn to an analysis of one
aspect of this.
Part II: Symmetry in the Assembly of the Polyhedra
1. The problem at Timaeus 55D-E
As noted in the introduction, the text of the Timaeus
at this point specifies sub-units, squares, and equilateral triangles,
which are more complicated than might be expected. A square can be
built from two isosceles right-angled triangles, but four are
specified; an equilateral triangle can be constructed from two
(30°,
60°, 90°) scalene triangles, but six are specified.
Cornford (1937) suggested that Plato’s
intention
was that many different constructions are to be understood for the
square and equilateral, all based on different numbers of the original
triangles, and that the text gives us only a ‘sample’ of each. This
proposal arises from another feature of Plato’s elements, that they
exist in various sizes with different properties (57C-D, 58C-D).
Cornford went further by proposing that in each case Plato’s sample is
the second member of a series which begins with the simpler
form. It is this second part of his proposal which presents problems,
since it is odd that Plato should give us no indication in his text
that this is his intention. In the subsequent literature the usual view
has been that of Zeyl (2000, p. lxviii), that there is still "something
of a mystery " as to why Plato chose the more complex scheme. Using
intuitive arguments, I have shown elsewhere (Lloyd 2006) that there is
no mystery; all the triangles specified are required, so long as the
symmetry of the final body to be constructed is considered at earlier
stages. This article includes a fuller survey of the literature than is
necessary here, and references to occasional suggestions by others that
symmetry might be significant for this problem; Rex (1989) also
indicates the importance of rotational symmetry.
An intuitive approach, based on visualization
of these polyhedra (‘bodies’, sômata, in Timaeus),
possibly including the examination of models, may well have been what
prompted the original constructions in the Timaeus.
Here I show that the same constructions also follow from an elementary
application of Group Theory, at the level of many undergraduate
chemistry courses. I do not intend to suggest that symmetry in its
modern sense is implied in the Timaeus; the word symmetria has
much more the sense of our ‘proportion’ than of ‘symmetry’. Here I
intend merely to demonstrate that, whatever the original reasons for
the choice, it was the correct one.[10]
Only by following Plato’s specification can polyhedra with the true
symmetry of the regular bodies be constructed. If the Timaeus
specifications are not followed, many isomeric forms result for each
size of each element, and some analysis of this problem is also
presented here. If they are followed, there is only a single
‘isomer’, a unique form.
2. Symmetry analysis
The majority of modern undergraduate textbooks
of
Inorganic and Physical Chemistry include a summary of the necessary
group theoretical language. I give a very brief introduction here,
generally following the approach of Shriver and Atkins 1999, pp. 117-8.
This reference may be consulted for further explanation, and more
detail is available in Harris and Bertolucci 1978, and in Cotton 1990.
The essence of the approach is to examine the complete set of symmetry operations
associated with some particular physical unit, often a molecule, but
here I apply it to four of the Platonic Solids and their constituent
triangles. This set of operations forms a group, which specifies fully
the symmetry of the unit. Knowledge of the mathematical properties of
any group, particularly as summarized in "Character Tables" (which give
traces of transformation matrices), allows wide-ranging rigorous
conclusions to be drawn about the physical properties of the unit
concerned. The operations transform the unit into exactly equivalent
configurations; they are associated with particular symmetry elements,
such as an axis of rotation, but the set of operations
constitutes the group.
The dimensionality of the triangles used by
Plato
is not immediately clear. A few commentators assume them to be at least
implicitly three-dimensional, but most have followed Aristotle,
accepting that they are true plane figures. The symmetry analysis is
simplified by ignoring any operations which involve the third
dimension; in any event the additional symmetries which would result
from including these are destroyed in the later assembly of the
polyhedra, since the inner and outer sides of the triangles then differ.
(a) The equilateral triangle
The Cornford construction of an equilateral
triangle by assembling two scalene triangles is shown in Figure 1a, and
that defined by Plato (Timaeus, 55D-E) is shown in Figure 1b.
Figure 1c shows an undivided triangle; this is converted to an
equivalent configuration by rotation about an axis, perpendicular to
the paper, through 120º. This can be repeated, and a third
repetition
regenerates the original configuration. The axis is called
‘three-fold’, and is labeled as C3. If there are no other
operations in the group, the same label is also used for the group;
specifications of labels for more complex cases can be found in the
above references.
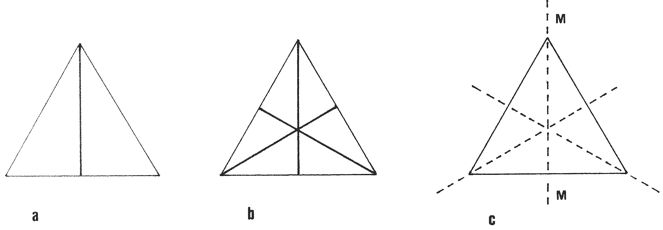
Figure 1. (a) Construction of the simplest
possible equilateral triangle, according to Cornford; (b) construction
according to Timaeus, 55D-E; (c) The mirror planes of an
equilateral triangle.
In addition to these rotation operations, such
a
triangle has left-right symmetries. The corresponding operation is that
of an imaginary mirror plane, again perpendicular to the triangle. The
mirror at MM in Figure 1c transforms all points in the right-hand half
into corresponding points in the left-hand half, and vice versa, and
there are two other such planes through the other vertices. All three
intersect at the same point, which is also the rotation center. The set
of all rotation and reflection operations specifies the group, one of
the ‘point groups’; the appropriate label is C3v.[11]
Further details of this and other point groups are given in the
references already cited.
We can also apply the operations of C3v
to the composite triangle of Figure 1b. We consider the join lines, the
only new feature of Figure 1b, as an ‘object’. However, this ‘object’
has exactly the same symmetry elements, and operations, as the
equilateral triangle, so it also has C3v symmetry. Thus the
mirror plane MM (see Figure 1c) converts the vertical join into itself,
and interchanges the other two. The other two mirror planes behave
similarly, and the ‘object’ also has three-fold rotational symmetry.
Thus the complete composite triangle behaves in exactly the same way as
an undivided equilateral triangle under the operations of the C3v
point group. When the composite triangle was assembled, it acquired the
full symmetry of an undivided triangle, and Plato’s construction,
Figure 1b, is completely equivalent to an undivided equilateral
triangle in symmetry terms. I have argued elsewhere (Lloyd 2006) that
Plato’s construction, 55 D-E, is equivalent to taking one of the
elemental triangles and successively operating on it, first with a
mirror plane, then with the 3-fold axis.
In stark contrast, Cornford’s triangle 1a has
a
much lower symmetry – only one reflection plane remains, and the point
group is Cs.[12]
(b) The tetrahedron
Assembly of a set of four equilateral
triangles (Timaeus, 54e-55a) generates the tetrahedron, with
point group Td.
The symmetry elements of the original triangles are now present in, and
operate on, the entire tetrahedron surface. Plato is only concerned
with faces, and not with the interior. If triangles according to Figure
1b are used for this assembly, then by the same argument as was used
above for the equilateral triangle, it follows that the point group of
the set of join lines over all four faces is exactly the same as that
of a tetrahedron with undivided faces, so that the Td
symmetry is unchanged by the presence of the join lines.
Some of the effects of the operations of the
symmetry elements can be seen in Figure 2. This shows a tetrahedron,
made up from Plato’s triangles (according to Figure 1b), in projection
down along one of the four 3-fold axes; faces 1-3 are facing the
viewer. The join lines on face 4, the base, are obscured by the three
faces above, but the operations of this 3-fold axis carry out the same
transformations as before on the base triangle.
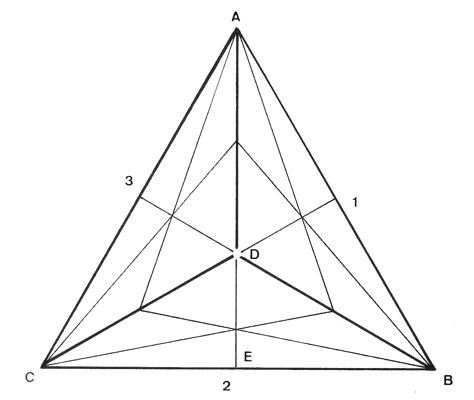
Figure 2. The tetrahedron ABCD shown in
projection,
perpendicular to the 3-fold axis which runs through D. Each side is an
equilateral triangle constructed as in Figure 1b.
A single rotation operation also transforms
face 1 with its set of join lines into face 2, etc. The mirror
plane passing through edges AD and DE transforms 1 into 3, and
exchanges the left and right halves of 2.
The operations of the elements of the
individual
faces on each other generate new symmetry elements of the
three-dimensional point group Td, the S4 axes.
These, which include two-fold axes, run through the centers of opposite
edges of the tetrahedron (and therefore of joins at triangle edges
according to Figure 1b), so their operations also transform the set of
joins into itself. In order to see this, it is useful to imagine the
tetrahedron inscribed in a cube (Figure 3a). The vertical S4
axis transforms edge AB into DC, and face 2, with the set of join
lines, into face 4, etc. Similar comments apply to the
operations of the other two perpendicular S4 axes.
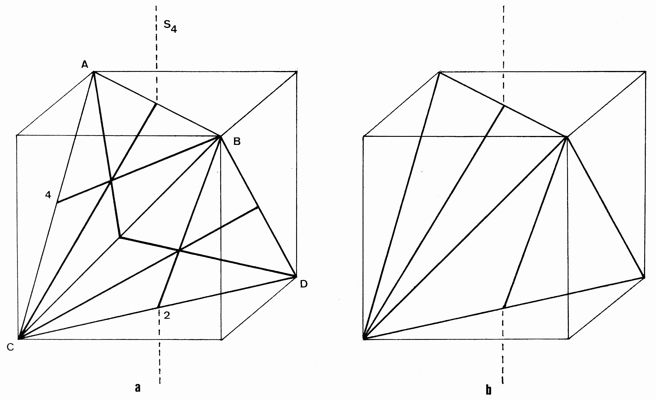
Figure 3. The operation of S4 axes
on
tetrahedra: (a) constructed from triangles according to Figure 1b; (b)
constructed from triangles according to Figure 1a.
However, any attempt to construct tetrahedra
using triangles according to Figure 1a fails to generate Td
symmetry. The best that can be obtained is D2d, shown in
Figure 3b. One S4
axis is retained, and this interconverts the four join lines, only two
of which are shown, into each other. However, the other S4
axes, and many of the other symmetry elements of the regular
tetrahedron (particularly those of the three-fold axes) have been lost.
In addition, so has the uniqueness of Figure 3a. All possible
orientations of all the triangular faces still give the same regular
tetrahedron for Figure 3a, but this is not so for Figure 3b, which
generates a variety of ‘isomeric’ forms.
(c) Isomers
There are very many forms of these
low-symmetry
tetrahedra, and the modern molecular concept of isomers is appropriate
to describe them. Each triangle according to Figure 1a can be set
independently in any of three orientations, so there is a total of 81
possible orientations. There are equivalent sets of these, which cover
several of the sub-groups of D2d. These sets can be
considered to arise from the equivalence of the regular tetrahedron
with respect to the x,y,z axes of Cartesian geometry; the two-fold axes
are conventionally aligned with these (in Figure 3 the z axis would
normally be vertical, so that it includes the S4 axis
shown). The general case is of an arrangement of joins which has no
symmetry, point group C1.
For any pattern of these joins seen from the +x direction, there is an
exactly equivalent pattern as seen from -x, which arises from a
different arrangement of join lines on the tetrahedron. The same is
true for y and z, so there is a set of six equivalent structures; this
is also true for Cs, C2 and S4
symmetries. If a structure does not have a reflection-rotation axis
(Atkins 1986, p. 409), as is true for C1, Cs and C2
symmetries, then there are also optical isomers, so that there is a
total of twelve for each set which has one of these symmetries.
However, in the case of the set of S4 type, there are only
six, since this cannot have optical isomers. For the D2d
type oriented along ±z, there is only one structure, since the
pattern
as seen from +z is identical with that from –z, and so there are only
three tetrahedra with this symmetry. By inspection[13]
the total of 81 is made up of six sets of twelve equivalent tetrahedra
(four of type C1, one each of Cs and C2),
one of six (S4), and one of three (D2d), giving a
total of eight distinguishable isomeric forms. From the Timaeus
text, it seems most unlikely that these multiple isomeric forms would
have been acceptable to Plato (Lloyd 2006).
(d) The octahedron and icosahedron
The octahedron constructed with triangles
according to Figure 1b has the full Oh symmetry of an
undivided octahedron. The three-fold axes of the triangles become the
four three-fold axes of the Oh
point group, running through opposite pairs of faces. Again, these
rotate the individual join lines in these faces into one another, and
rotate the other six faces, with their join lines, into each other. The
mirror planes of the triangles remain, and new ones are created in the
assembly of the octahedron, which run through edges. In projection onto
a plane perpendicular to a four-fold axis, the outline becomes a
square. Each operation of the four-fold axis rotates each triangle,
with its join lines, into the next one (compare the operation of the
3-fold axis in Figure 2; an illustration of the operation of the 4-fold
axis is given in Lloyd 2006 as Figure 9). The mirror planes coincident
with edges also interchange all triangles, whereas those which divide
faces carry out the same operations on these as they do on the
constituent triangles, and interchange the other faces. The analysis
can be continued to all the operations; in every case the join lines
are converted to equivalent configurations.
However, if triangles according to Figure 1a
are
assembled, the highest possible symmetry, with all the join lines
oriented towards one of the four-fold axes, is D4h. A
structure of this type has appeared in the discussion of the
Cornford-derived polyhedra shown in Friedlander 1958 and also in
Vlastos 1975 (pp. 69-79), but apparently without the low symmetry
having been noticed. Possible reasons for the loss of symmetry not
being detected earlier are discussed in Lloyd 2006. There are many more
isomers than for the tetrahedron.
Similarly, a unique, completely regular
icosahedron, with point group Ih,
can be assembled from triangles according to Figure 1b. However, the
maximum symmetry accessible if triangles according to Figure 1a are
used is D5d. This low-symmetry object has been illustrated
in Vlastos 1975 (Figure 4, p. 76); again there are very many isomers.
(e) The square and cube
A true square has C4v symmetry, if
we restrict the operations to two dimensions, and this is also true of
Plato’s specification in Timaeus
(55B-C) as one made up from four right-angled isosceles triangles
(Figure 4b). Cornford’s ‘simpler’ square (Figure 4a) has a symmetry
reduced to C2v. The point group of the regular cube is Oh,
and this follows automatically for a cube constructed from the
four-component (C4v) square. However if the two-component
square is used, several symmetries are possible, of which the highest
is D3d.
This can be obtained in two different arrangements, one of which is
probably implied in the left-hand item in Figure 6 of Vlastos 1975 (p.
78). Lower symmetries produce many different isomers, so the square in
Figure 4a is no more suitable for building a unique symmetric cube than
is the triangle in Figure 1a for building fully symmetric deltahedra.
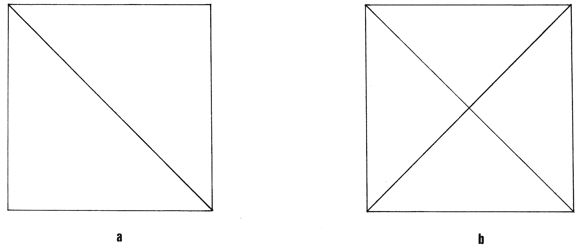
Figure 4. Construction of the simplest square
from isosceles right triangles: (a) according to Cornford; (b)
according to Timaeus.
3. An alternative approach
Rather than first constructing the equilateral
triangles (squares) of the faces, it may be appropriate to begin with
the Platonic solids, with each face divided as above. Professor P. W.
Fowler has pointed out that the full Platonic schemes for the
tetrahedron, octahedron, and icosahedron, using triangles according to
Figure 1b as faces, in each case generate the regular representation of
the appropriate group. (A brief description of the language used here
is given by Fowler and Quinn (1986)). The individual scalene triangles
are irreducible regions, transformed into each other (permuted) by the
operations of the particular group; any point within one of these
triangles, when operated on by the group, generates the regular orbit.
The regular representation has a character under the identity equal to
the order of the group, so that the number of elementary triangles is
equal to the number of operations, i.e. 24 for the tetrahedron,
48 for the octahedron, and 120 (as is specified by Plato at 55A-B) for
the icosahedron. This provides a very economical demonstration of the
point established rather more laboriously above, that Plato’s method
for constructing the faces of these deltahedra generates bodies with
the full symmetry of the regular, undivided bodies.
The argument is not exactly analogous for the
square used at 55B, since the isosceles triangles used in Figure 4b are
not irreducible units; to generate the regular representation, all four
of these triangles have to be divided along the bisecting mirror planes
of the square. Plato’s construction here uses pairs of these
irreducible units. It would probably have seemed unnecessary to him to
make this final division, since the square according to Figure 4b is
adequate for his declared purpose of using an isosceles triangle
(54A-B) as the basic unit.
4. Larger species
It was noted in the Introduction that Plato
requires
various sizes of each of his elements; this was Cornford’s original
motivation for his set of constructions. The first of these, as in
Figure 1a (or 4a) has too low a symmetry, or, equivalently, it does not
follow Plato’s construction methods at 54D-E and 55B-C. Nevertheless,
Cornford’s argument that Plato intended his readers to understand that
the different sizes of triangles were all made up from combinations of
the same basic units is unaffected by this. The only stipulation must
be that such larger units can create polyhedra which have the full
symmetry of the appropriate point group. I have shown elsewhere (Lloyd
2006) that there are composite triangles, of increasing size, which
satisfy this condition. That there must be some larger suitable
triangles is most readily demonstrated, in the context of Section 3
above, by the observation that any individual scalene triangle in one
of the deltahedra is an irreducible region of the polyhedron. This is
equally true if each scalene triangle is a composite, built up from
smaller units. Any such composite scalene triangle, with angles of
30º,
60º, and 90º, can be used as the irreducible unit. The
operations of
the point group on this will generate first a large equilateral
triangle of the type of Figure 1b, and then the regular polyhedron. The
first of these composite scalene triangles has three components (Figure
1b can be thought of as made up of two of these, divided by the plane
MM), and the next has four. The figures in Cornford 1937 on pp. 236-7
develop some equilateral triangles which are made up in this manner,
and these inevitably have the correct C3v symmetry. However
his method of constructing equilateral triangles also generates many
which cannot be decomposed into a set of six equivalent scalene
triangles, and have a lower symmetry. In contrast, Plato’s construction
at 55D-E, summarized in Figure 1b, can be used to generate any desired
size of equilateral triangle by choosing an appropriate composite
scalene triangle: all equilateral triangles developed by this method
have to be suitable for constructing truly regular deltahedra. Similar
comments apply to larger squares. With this set of larger triangles and
squares, the many different elements which are required by Plato’s
scheme for chemistry can be constructed.
Conclusions
Visintainer’s suggestion of dividing the
elemental triangles is at variance with the text of the Timaeus,
with the evidence of Aristotle, and with a variety of comments in the
literature. His argument for a continued division, based on Timaeus
57D, is not sustainable; this text cannot carry the meaning attributed
to it. There is no reason to suppose that Plato would have thought it
in any way necessary, desirable, or even possible to have a division of
one of his elementary triangles. The proposal, or ‘assertion’, ascribed
to Cornford, that there are two, and only two, minimally sized
triangles in Plato’s scheme, of finite size, can stand. The attack on
Cornford’s approach would, if successful, have demolished his
particularly significant ‘building block’ idea, of constructing larger
triangles by assembling various numbers of the minimal stoicheia;
this idea is unaffected.
However, in putting forward his particular
scheme,
Cornford (1939, p. 237) poses the question: "Why, then, did Plato
analyze his equilateral face into six elements, which have less prima
facie claim
to perfection [than a simple equilateral triangle]?" The result of the
symmetry analyses above is that the six-fold unit has precisely the
‘perfection’ of the simple equilateral triangle, and is therefore
appropriate to construct truly regular polyhedral elements, of symmetry
Td, Oh or Ih. This is not true
of Cornford’s proposed two-fold unit, the triangle in Figure 1a. Use of
this smaller unit leads both to asymmetry and to multiplicity, to
‘isomers’, for all three deltahedra. Exactly parallel comments apply to
the squares and cubes generated from them. The argument can also be
extended to include larger polyhedra, so long as Plato’s constructions
are adhered to. It is implicit in this that there is only a need for
one size of each of the two types of elementary triangles. Cornford’s
principle of using ‘building blocks’ to assemble the faces of larger
polyhedra, which form the various sorts of each type of element, gains
further support from this.
Acknowledgements
I thank Mr. M. Bispham for drawing my
attention to the paper discussed above, and Professor D. Sedley, for
helpful and incisive comments on the work of Part I. I am also grateful
to Professor P.W. Fowler for providing the ideas of section 3 of Part
II, and to Professor C.M. Quinn for helpful comments on aspects of
symmetry and isomers, and for provision of an unpublished manuscript.
Notes
[1] Throughout
this paper I
use the translation by Zeyl (2000), unless otherwise specified, and I
refer to the accompanying commentary, as well as to those of Cornford
(1937) and Taylor (1928).
[2] The reception
of the text in
antiquity is summarized by Zekl (1992, pp. lxxi-lxxiii). Zeyl (2000),
gives a historical perspective leading up to the present day, see
particularly pp. xiii-xv.
[3] Plato would
not consider the term ‘element’ appropriate for describing his bodies
(see Timaeus
48B-C) because he does not believe that these are fundamental, but the
convention is so well established that I will use it here.
[4] Possibly in
other languages
also. Zekl (1992, p. xiv) states that his extended essay and extensive
notes to his translation do not constitute a commentary to replace
Cornford 1937 and earlier commentaries.
[5] See in
particular Zeyl 2000,
where there is no indication that there are alternative views. For
alternatives, see Mugler 1960, pp. 21-26; Böhme 2000, p. 308;
Brisson
2001, pp. 303-6. These will be discussed elsewhere.
[6] There is of
course an earlier
mention of division of a surface into triangles, and dividing these
into right-angled triangles, at 53C-D. However, this is establishing a
general point about the nature of plane surfaces, not an invitation to
divide these right triangles further.
[7] Mugler (1960)
has made a
similar claim to Visintainer about the interpretation of the Greek
text, but this has been strongly criticized by O’Brien (1984).
[8] Here Cornford
1937 has the
disconcerting translation "the number of these differences being the
same as that of the varieties in the kinds". If taken literally, this
is mathematical nonsense, but the word ‘difference’ is unnecessary.
Archer-Hind 1888 has "and there are just so many sizes as there are
kinds in the classes", Bury 1966 "of sizes as numerous as are the
classes within the Kinds", and Jowett 1892 "there are as many sizes as
there are species of the four elements". Cornford’s ‘difference’ can
only be interpreted as meaning ‘different sort’.
[9] My italics;
the original reads "suivant les côtés des triangles
rectangles" (Bruins 1951, p. 279, ‘Remarque’).
[10] Nevertheless,
it may be
noted that Brisson (2003) has suggested that Plato may have had some
idea of our axis of symmetry; he writes (p.14): "on peut cependant
penser que […] Platon veut trouver un centre de symétrie
axiale". I
have argued elsewhere (Lloyd 2006) that passages from Plato’s nephew
Speusippus suggest some sort of awareness of our ‘symmetry’ concept.
[11] If the
additional operations in three dimensions are considered, this becomes D3h
.
[12] C2v
if the additional operations in the third dimension are considered.
[13] The device
of the
stereographic projection (Harris and Bertolucci 1978, pp 17ff.) is
useful in working through these different structural types.
References
Archer-Hind, R.D.: 1888, The Timaeus of
Plato, London: Macmillan.
Atkins, P.W.: 1986, Physical Chemistry, 3rd
edn., Oxford: Clarendon.
Black, J.A.: 2000, The Four Elements in
Plato’s Timaeus, Lewiston: Mellen Press.
Böhme, G.: 2000, Platons theoretische
Philosophie, Stuttgart and Weimar: Metzler.
Böhme, G. & Böhme, H: 1996, Feuer,
Wasser, Erde, Luft: eine Kulturgeschichte der Elemente, Munich:
Beck.
Brisson, L: 2001, Timée,Critias, 5th
edn., Paris: Flammarion.
Brisson, L: 2003 ‘À quelles conditions
peut-on parler de "matière" dans la Timeé de Platon?’,
Revue de Métaphysique et de Morale, 14, 5-21.
Brisson, L., & Meyerstein, F.W.: 1995, Inventing
the Universe, Albany: SUNY Press.
Bruins, E.M.: 1951, ‘La Chimie du
Timée’, Revue de Métaphysique et de Morale, 56,
269-282 [an English translation, with some corrections to the French
text, appears in Black (2000), pp. 73-89].
Bury, R.G.: 1966, Plato / with an English
translation. Timaeus – Critias – Cleitophon – Menexenus – Epistles,
Cambridge, MA: Harvard University Press.
Cornford, F.M.: 1937, Plato’s Cosmology,
London: Routledge and Kegan Paul.
Cotton, F.A.: 1990, Chemical applications
of group theory, 3rd ed., New York: Academic Press.
Friedländer, P.: 1958, Plato,
translated from the German by H. Meyerhoff, Princeton: Princeton
University Press.
Gregory, A.: 2000, Plato’s philosophy of
science, London: Duckworth.
Harris, D.C., & Bertolucci, M.D.: 1978, Symmetry
and Spectroscopy: an introduction to vibrational and electronic
spectroscopy, Oxford: Clarendon.
Jowett, B.: 1892, The Dialogues of Plato,
London: Macmillan [reprint: Mineola NY, Dover, 2003].
Lloyd, D.R.: 2006, ‘Symmetry and Asymmetry in
the construction of ‘Elements’ in the Timaeus of Plato’, Classical
Quarterly, 56, 459-471.
Mugler C.: 1960, La Physique de Platon,
Paris: Librairie C. Klincsieck.
O’Brien, D.: 1984, Theories of weight in
the ancient world: four essays on Democritus, Plato and Aristotle: a
study in the development of ideas, Paris: Les Belles
Lettres & Leiden: Brill, Vol. 2 (Plato, weight and sensation:
the two theories of the ‘Timaeus’).
Rex, F.: 1989, ‘Die Älteste
Molekülartheorie’, Chemie in unserer Zeit, 23,
200-206.
Shriver, D.F., & Atkins, P.W.: 1999,
Inorganic chemistry, 3rd edn., Oxford: Clarendon.
Sorabji, R.: 1983, Time, creation and the
continuum: theories in antiquity and the early Middle Ages, London:
Duckworth, pp. 358-9.
Taylor, A.E.: 1928, A Commentary on
Plato’s Timaeus, Oxford: Clarendon.
Visintainer , J.: 1998, ‘A Potential Infinity
of Triangle Types: On the Chemistry of Plato’s Timaeus’, Hyle:
International Journal for Philosophy of Chemistry, 4, 117-128.
Vlastos, G.:1975, Plato’s Universe,
Oxford: Clarendon.
Zekl, H.G.:1992, Timaios:
griechisch-deutsch, Hamburg: Meiner.
Zeyl, D.J.: 2002, Timaeus,
Indianapolis: Hackett.
D. Robert Lloyd:
Chemistry Department, Trinity College, Dublin 2, Ireland; dlloyd@tcd.ie, boblloyd@waitrose.com
Copyright © 2007 by HYLE and D.
Robert Lloyd
|