HYLE--International Journal for Philosophy of Chemistry, Vol. 4 (1998), No. 2 , pp. 117-128
Abstract: Francis Cornford's assertion that there must be a smallest elemental triangle in the Platonic chemistry of the Timaeus is overturned in this paper. I show that, according to Plato, there need not be such a triangle and there might be a potentially infinite amount of elemental triangles. In doing so, I follow the interpretation of the Platonic chemistry first proposed by Bruins. Finally, I draw some conclusions with regard to Plato's relationship to atomism and modern chemistry.
Keywords: ontology, Plato's chemistry, atomism, elements,
perfect solids.
The chemistry of the Timaeus might appear as an arcane curiosity and nothing else at first glance. Through the eyes of any Twentieth Century student of science and metaphysics, Plato's chemistry seems at odds with contemporary chemistry. For example, we know that there are more and other elements than the four (fire, air, water, and earth) that Plato claimed. And, certainly, we do not claim that the perfect solids or triangles have anything to do with the way that elements are formed or the way that chemical reactions take place.
However, Plato's ideas appear more tenable when we consider that the way that reactions take place in the Platonic chemistry are analogous to the way that chemical reactions are said to take place by modern chemistry. When water is converted into air in the Platonic chemistry, the molecules of water (which are comprised of the perfect solid icosahedron) must be comprised of faces (which are triangular) that are, ultimately, reconcilable (of the same size as) the triangular faces of the molecules of air (which are comprised of the perfect solid octahedron). On Plato's view it is clear that chemical reactions can take place only when a specific set of necessary variables (on Plato's view, the size of reacting triangle faces) are met. Similarly, in modern chemistry, certain sets of variables must be met in order for reactions to take place. For example, in order for hydrogen and oxygen to react to make water, it is not sufficient that hydrogen and oxygen just be proximate to one another. Specifically, 2H2 + O2 « 2H2O, i.e. we must have two molecules of free hydrogen to one molecule of free oxygen in order for the reaction to take place. The 'discrimination' shown by molecules in modern chemistry is certainly analogous to the 'discrimination' shown by the perfect solids and their constituent triangles in the Timaeus. This similarity has led at least one author to claim that the chemistry of Plato's Timaeus is indeed the first molecular theory in the history of chemistry,[1] and I would be hard pressed to disagree that, at least, Plato's theory is a great speculative advancement in the history of chemistry.
I think that one of the most important goals of ontology is to determine what the ultimate nature of the world actually is, and Plato's contribution toward that end cannot be gainsaid. His attempts would be instructive even if they were merely erroneous historical curiosities, but these attempts are not merely curiosities. Plato's chemistry and ontology does in fact appear to have a certain tenability. To that end I must also cite the work of Francis Cornford (1937) in the area of the chemistry of the Timaeus as very influential. Cornford showed how the triangle has the utmost importance in Plato's chemistry, and he showed how Plato's chemistry, with its reliance on triangles, can be considered as a great speculative chemical system.
In this essay, I will examine why the ultimate building blocks in this
system - the triangles - are not given any definite size by Plato.
Although Cornford insists that Plato must hold that there must be a smallest
triangle, which would stand as the ultimate in Plato's chemistry, I will
argue that Plato need not have such a smallest triangle. I will instead
make a case that all the triangles that exist as the faces of the regular
solids can be divisible in principle, and, therefore, we could have ever
smaller triangles in principle. In other words, I will show how Plato's
chemistry need not have a smallest elemental triangle.
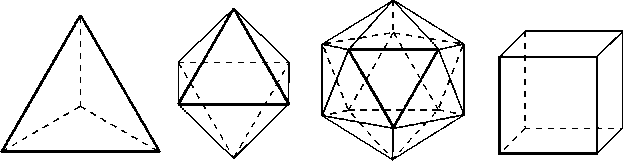
Let us begin with what Plato states of the chemistry in the Timaeus. We are told that there are four and only four solids which comprise the objects of the universe (Fig. 1). First, there is fire. This element has the form of the tetrahedron. Then air, which takes the form of the octahedron. Third is water, which takes the form of the icosahedron. Finally, there is earth, which has as its form the cube.[2]

Figure 1. Plato's regular solids: tetrahedron (fire), octahedron (air), icosahedron (water), cube (earth).
The perfect solid 'dodecahedron' is eliminated from Plato's chemistry. Why does it have no place here? Well, for one thing, there is only fire, air, water, and earth in Plato's Timaeus, and the dodecahedron is left out simply because it would correspond to a non-existent fifth kind. Furthermore, Plato inherited (from the Pythagoreans) a view that the dodecahedron possessed a peculiarly ethereal nature. We could say that the dodecahedron simply has no place in the mundane realm of fire, air, water, and earth.[3] However, it will become clear shortly why the dodecahedron, with its twelve faces of regular pentagons, will be impossible to incorporate into the Platonic chemistry.
Now, even though Plato is explicit that there are four and only four elemental solids, he is quick to posit that there are many different kinds of these solids. What differentiates the different kinds of fire, air, earth, and water from one another? This question must be asked, because if the ultimate nature of fire, for example, is to be tetrahedral, then how could one type of perfect tetrahedron be different from another? Plato answers these questions by asserting that differences in type between kinds of fire are caused only by the sizes of the regular solids themselves (in this case, difference in size between the tetrahedrons). Given the fact that there is no difference between, for example, two regular tetrahedrons except their sizes, we can conclude that the only thing that could account for the diversity of types of fire (in this case) would be their sizes.
We can state with certainty that there must be a limit to which the regular solids can be large. This conclusion follows from the fact that Plato states, we "must think of all these bodies as so small that a single body of any one of these kinds is invisible to us because of its smallness […]” (Timaeus, 56b-c). From Plato's statement it follows that we cannot have a type of fire whose properties are determined by the fact that its faces have an area of, say, 2 square centimeters. Because, in that case, we would have a type of fire whose properties are borne out by being a tetrahedron that is necessarily visible to the naked eye. It is therefore clear that Plato's endless diversity of sizes of triangles (which elementally comprise the two-dimensional 'atoms' from which the solids are made, as we shall see shortly) does not approach the infinitely large, because then it would be necessary to have types of fire, air, water, and earth that are, in their elemental geometrical structure, visible to the naked eye.
Now while the limiting large size of the triangles is now clear, it
is not clear what their limiting size should be as regards smallness. In
fact, we are led to believe that there might be no real limit to the smallness
of the triangles that constitute the types of the elements because of Plato's
call for an 'endless diversity' of elemental triangles.[4]
There are two ways in which we can now proceed:
Case 1 allows for regular solids that become smaller and smaller. On this view, one type of triangle x is identified with its particular size, and another type of triangle y is identified with its size. Now, at some point a triangle becomes so large that it is visible to the naked eye, so we have a definite limit for the largeness of triangles that would constitute particular solids. However, Plato has indeed called for the 'endless diversity' of types of triangle, so we might be inclined to conclude that the only way to ensure such an indefinite variety of types of triangle would be to proceed toward the infinitely small elemental triangle.
Now consider Case 2. Cornford presents a way how a certain number of of triangles can be derived: Take a regular tetrahedron j whose equilateral triangular faces are all of a certain size. Also, take another regular solid, an octahedron k whose faces are smaller in area. We now have two regular solids whose triangular faces seem to be irreconcilable for the Platonic chemistry (Fig. 2).
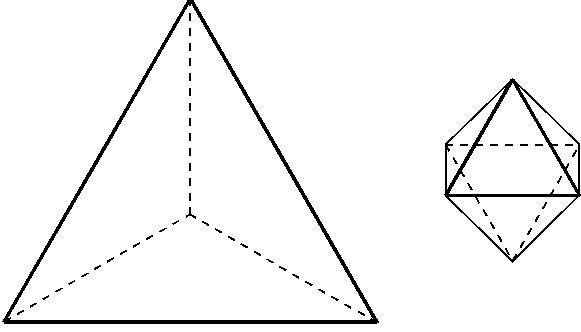
Figure 2. A tetrahedron j and an octahedron k with apparently irreconcilable equilateral faces.
Yet, this discrepancy is just what Cornford calls for. We should ask, how could these two regular solids ever react with one another? Cornford seems to be pushing for a view whereby the tetrahedron and the octahedron both must 'disintegrate' into their constituent equilateral triangular faces of differing sizes x and y.[5]
Then, the resultant 'free' equilateral triangles must in turn disintegrate into their right scalene triangles (Fig. 3).[6]
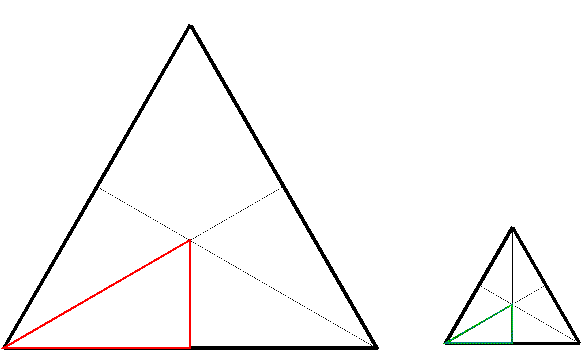
Figure 3. Disintegration of the two equilaterals of Figure 2 into right scalenes (x left, y right).
Now, in the case I have just presented, it would seem that all of the right scalene triangles that result from the trisectioning of equilateral triangle x could not be of the same areas as those that result from the trisection of equilateral triangles of the y type (Fig. 4).
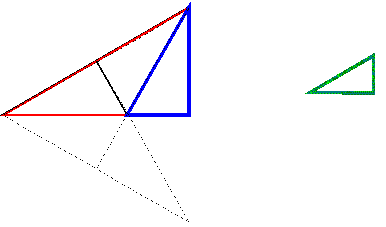
Figure 4. Two right scalenes from the disintegration of the right scalenes of Figure 3, still irreconcilable.
So, in order for tetrahedron j to be reactive with octahedron k, their elements must be found at a 'lower level'. The elemental right scalenes must be found after a finite number of divisions of right scalenes (Fig. 5).[7]
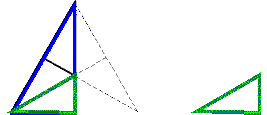
Figure 5. Reconcilable right scalenes are, eventually, found after a finite number of divisions.
Thus, a tetrahedron and an octahedron of different face sizes might react with one another.
Now, the cube's faces are squares made from half-squares (triangles). Just as in the case of tetrahedron, octahedron, and icosahedron, there are a variety of cubes which correspond to a variety of types of earth. Cornford shows how cubes of differing sizes could react with one another. First, take a cube with faces of size m. Take another cube with faces of size n, larger than m (Fig. 6).
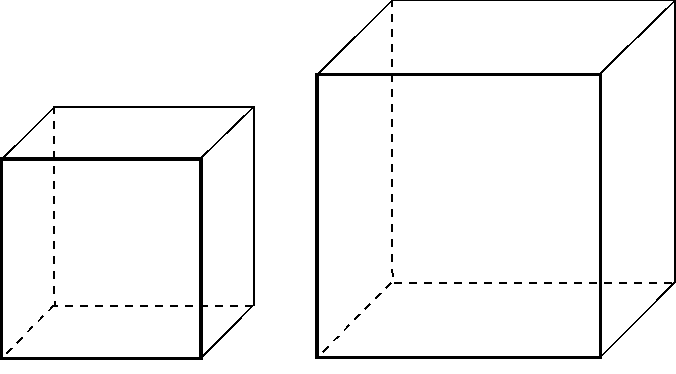
Figure 6. Two irreconcilable cubes (m left, n right).
These two square faces m and n can be broken up into half squares, and these half squares can again be broken up into half squares until we reach Cornford's atomic half square (Fig. 7).[8]
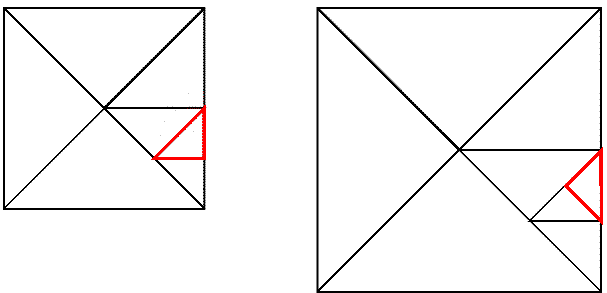
Figure 7. Reconcilable half-squares can be found after a finite number of divisions of the cube faces of Figure 6.
So, we see how a cube with faces of size m could react with a cube with faces of size n. The similarities of the reactions of right scalene triangles and half squares is obvious.
Case 2, as just illustrated, is Cornford's view on the chemistry of
the Timaeus. I will now show how his account is unsatisfactory.
Cornford states that the process of dividing any given equilateral triangle into 6 right scalenes, and then dividing any of the resultant right scalenes into 3 right scalenes, and so on "[…] can be carried on ad infinitum. Plato, however, does not continue the process indefinitely. He stops at a minimum triangle […] of each type, which is taken to be atomic. He then builds the […] equilateral out of 6 half-equilaterals.”[9]
There is a problem with Cornford's assertion. Plato never explicitly states that the process of division of equilateral triangles does not continue indefinitely. When Cornford says that the subdivision of triangles should not proceed ad infinitum, he is commenting on Timaeus 57d-e. I have cited this passage previously, and there simply is nothing here in the Timaeus that precludes such a potential infinite divisibility.
Moreover, without this potential infinite divisibility, we simply cannot account for an endless diversity of elemental triangles. First, if we are to follow Cornford's demand that there must be an elemental right scalene triangle which is never divisible in actuality, then it must be of some size x. We know that Cornford's program calls for various roles for such an elemental triangle of size x: First, it could remain by itself and form just a right scalene triangle. Second, it could combine with another right scalene triangle of size x to form an equilateral triangle. Third, 6 right scalenes of size x could combine to form an equilateral triangle. Last, the right scalene of size x could combine with other right scalene triangles to form patterns of triangles (Fig. 8).[10]
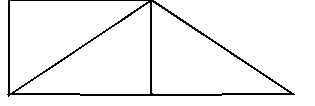
Figure 8. All three triangles are of same size x.
Notice that for any such pattern, there are a finite number of 'real Cornfordian triangles' in it, because we still cannot actually divide any of the elemental right scalenes of size x.
I have said before that the elemental right scalene of size x
has to be of a certain magnitude in order for the solids to have any size
at all. So, Cornford's program leads us into a difficulty. No matter how
small the elemental right scalene of size x is, we shall very shortly
have on our hands amalgamations of elemental right scalene triangles that
are visible to the naked eye. If Cornford's assertion that there
are right scalene triangles that are impossible to break-up in actuality
is correct, then Plato's chemistry is flawed. The "endless diversity”
of triangles that Plato explicitly mentioned could not be gained in the
case that we were to follow Cornford's assertion that Plato would not allow
for possible further divisions of elemental right scalene triangles of
size x.
What, then, is to be gained from overturning Cornford's assertion? I think that we can account for the "endless diversity” of sizes of triangles if we allow for potential divisibility ad infinitum. I follow Case 1 - the view of potential division down toward the infinitely small.
Plato knows "various” kinds of fire, air, water, and earth, but he considers an "endless variety” of types of elemental triangles. We could interpret Plato in the following way. Fire, air, water, and earth are, in some sense, of a different ontological order than their constituent triangles. Fire burns us, and we breathe air. In our everyday experience we encounter many 'sorts' of 'things'. Plato is well aware of this fact, and thus he introduces kinds of fire, air, water, and earth. As we have already seen, the differences between these kinds come about only through the sizes of the regular solids. Of course, it happens that in everyday experience we encounter only a finite number of the kinds of fire, air, water, and earth.
Cornford might have been influenced by Plato's assertion that, "[…] the first of the elemental triangles ceased acting when it had generated [… its] three solids, the substance of the fourth Kind [the cube] being generated by the isosceles triangle” (Timaeus, 55b-c). This statement seems to imply that the right scalenes and the half square triangles form triangles that are atomic. However, that view is not the only possible interpretation of this passage.
Instead, we could say that right scalenes, at some time, combine to form equilaterals (Fig. 9) of which the tetrahedron, octahedron, and icosahedron are made.
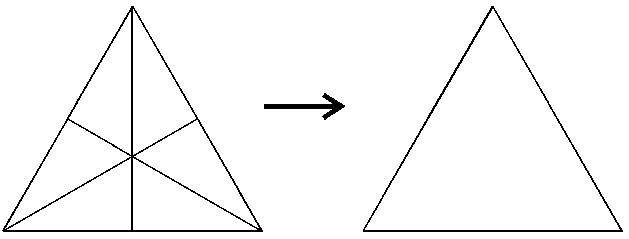
Figure 9. Equilateral made from right scalenes.
Then, following the scheme of Bruins (1951), we could see how, for any given equilateral triangle, it could become itself a tetrahedron, given that it should 'cut itself' in the correct way and 'fold out' into the third dimension (Fig. 10).[11]
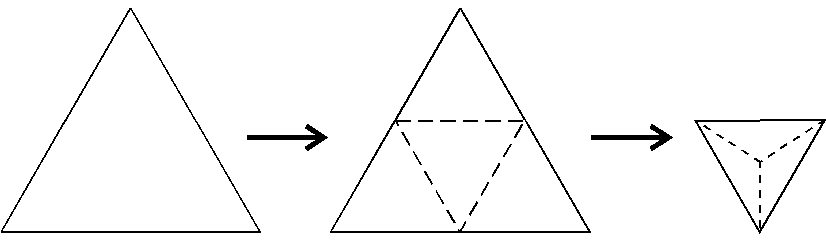
Figure 10. The Bruins program for the formation of tetrahedrons (fire).
The reaction shown above is the conversion of triangles that comprised an octahedron into tetrahedrons, for example. So, even though we remain faithful to the Platonic insistence that the "first of the elemental triangles ceased acting when it had generated [tetrahedrons, octahedrons, and icosahedrons]”, we still allow the possibility of tetrahedrons, octahedrons, and icosahedrons comprised of faces smaller in area than the original elemental right scalene triangles.
Also, Bruins' interpretation of the chemistry allows for smaller and smaller cubes.[12] We can imagine cubes that have faces lesser in area than original elemental half squares.

Figure 11. Seemingly irreconcilable square and half-square.
Now, it should be obvious how such cubes could be created. Half-squares could be broken down to smaller half-squares, and then a cube smaller than its original half-square might be created.
It might appear at first glance that my interpretation here does not
address the very problem of how transformations take place generally between
differing sizes of triangles. Cornford seemed to be addressing and accounting
for that problem by making one particular size of triangle atomic, thereby
limiting the potentially astronomical varieties of types. Encounters between
reconcilable types seem to be more probable then. My view places no such
limit on the number of triangle types. Reconciliation between differing
sizes of solids must then be accounted for by some kind of uniformity and
proportionality of nature. It must then be the case that triangles of similar
types naturally occur without Cornford's speculative prohibition
on types not conforming to his atomic triangles. If I am right, then Plato's
view squares with contemporary chemistry in that no speculative constraints
need be put on types of atoms or elements. It is just the case that water
(the compound as we know it today) is generally formed the way that it
is formed. Rarer combinations are possible (like hydrogen peroxide), and
some combinations that are possible in thought (like a compound of krypton
and argon) still do not occur in nature. That some reactions are common
and do take place is not simply ruled by combinatorics. Plato's chemistry
can be seen to include triangles that commonly make certain compounds for
no good reason other than the fundamental working of nature allows for
certain sizes of triangles more commonly than others.
My view of Plato clearly distinguishes him from his contemporary atomists. In my interpretation, it is clear that no actual triangle (be it a right scalene or a half square) can rightly be called the atom from which all triangles and, ultimately, elemental solids are made. But it could be said that the particular types of water and air that we find in our everyday universe are elemental on Plato's view. That there could not be rare types of elements made from rare triangles is not precluded on my view, however. Similarly, in modern science the rarest elements are made from atomic structures that, although sometimes unstable and very rare, might still exist, at least in principle (consider the elements californium and plutonium for example). Plato is in step with modern science on that point.
Also, consider the Platonic chemistry in regard to the drive toward the discovery of new and rare compounds. On Plato's view, there is a ban on macroscopic cubes, tetrahedrons, icosahedrons, and octahedrons, but it is possible to interpret the Platonic chemistry as allowing for - in principle at least - larger and larger atomic solids. Plato's chemistry, when allowed to have an indefinite number of potential elemental triangles, can be seen as a great influence in the progress of chemistry. We can speculate that certain sizes of triangles are very rare, and even non-reactive (much like the noble gases). Such substances would be rare - certainly as solids get larger and larger in the Platonic chemistry, the prohibition on macroscopic solids calls for a certain instability. It could be the case that it just happens that the certain sizes of triangles needed for reactions generally exists, and Cornford's call for a definite smallest elemental triangle was actually made to account for the reactions to take place, but my view handles reactivity in a different way.
In any case my interpretation allows an indefinite number of classes
within the kinds of fire, air, water, and earth. There could be certain
definite types of water, for example, that are commonly found in our everyday
experience, such as gold, and there could be other definite types for the
other elements. As we encounter smaller and smaller types of tetrahedrons,
we encounter differing types of fire. Although Plato's chemistry allows
for an indefinite number of classes within the kinds, this does
not imply that there actually are infinitely many classes within
the kinds in the universe. My interpretation allows for an endless diversity
of sizes of elementary triangle, as well as an endless diversity of classes
within the kinds of elements.[13]
Bruins, E.M.: 1951, 'La Chimie Du Timee', Revue de Metaphysique et de Morale, 56, 269-282.
Cornford, Fr.: 1937, Plato's Cosmology, Routledge and Kegan Paul, London.
Diels, W. & Kranz, H.: 1952, Die Fragmente der Vorsokratiker, 6th ed., Berlin.
Friedländer, P.: 1949, 'Structure and Deconstruction of the Atom According to Plato's Timaeus', University of California Publications in Philosophy, 16, 225-248.
Heisenberg, W.: 1970, Natural Law and the Structure of Matter, Rebel Press, London.
Plato: 1989, Timaeus, trans. R.G. Bury, Harvard University Press, Cambridge.
Rex, Fr.: 1989, 'Die Älteste Molekulartheorie', Chemie in unserer Zeit, 23, 200-206.
Copyright Ó1998 by HYLE and John Visintainer