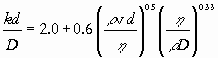
Keywords: modeling, chemical engineering, similarity considerations, dimensional analysis, ceteris paribus conditions.
As a simple example consider two lengths of smooth tubing, one of which
is 1 cm in diameter and 100 cm long (the model), and the other 1 m in diameter
and 100 m long (the prototype). In general, the model and the prototype
will display similar behavior if, for the same boundary conditions, the
relevant dimensionless groups such as the Reynolds number have the same
value for model and prototype. Examples of dimensionless numbers and the
dimensional variables that enter into them are given in Tables 1 and 2.
| Re | Reynolds number | ratio of inertia and viscous forces | rdv/h |
| Fr | Froude number | ratio of inertia and gravity forces | v2/gd |
| Nu | Nusselt number | ratio of total and molecular heat transfer | hd/l |
| Sh | Sherwood number | ratio of total and molecular mass transfer | kd/D |
| Pr | Prandtl number | ratio of molecular and momentum heat transfer | hC/l |
| Sc | Schmidt number | ratio of molecular and momentum mass transfer | h/rD |
| Fo | Fourier number | dimensionless time characterising heat flux into a body | lt/rCd2 |
| ƒ | Fanning friction factor | dimensionless pressure drop | dDP/2Lrv2 |
| jH | Colburn j factor | dimensionless heat transfer coefficient | NuRe-1Pr-0.33 |
| jM | Colburn j factor | dimensionless mass transfer coefficient | ShRe-1Sc-0.33 |
| real numbers | a, b, c | [-] |
| heat capacity | C | [H/MT] |
| diameter | d | [L] |
| molecular diffusion coefficient | D | [L2/t] |
| gravitational acceleration | g | [L/t2] |
| heat transfer coefficient | h | [H/tL2T] |
| mass transfer coefficient | k | [L/t] |
| permeability of porous medium | K | [L/t] |
| length | L | [L] |
| pressure difference | DP | [M/Lt2] |
| overall liquid velocity | q | [L/t] |
| time | t | [t] |
| Cartesian coordinates | x, y, z | [L] |
| velocity | v | [L/t] |
| viscosity | h | [M/Lt] |
| porosity | e | [L3/L3] |
| thermal conductivity | l | [H/tLT] |
| cake resistance | Q | [t/L] |
| density | r | [M/L3] |
The concept of similarity extends to many characteristics besides geometry. For example, in aeronautical engineering it may be specified that the mass distribution in a model be similar to that in the prototype or that the ratio of stiffness of homologous cross sections of a prototype wing and a small-scale model must be constant. Often scale effects are difficult to eliminate. For example, the surface of a material that is relatively smooth on the prototype scale may be ‘rough’ on the model scale. In chemical engineering, in addition to dimensionless numbers for fluid flow, dimensionless numbers for heat and mass transfer are of crucial importance. A simple example illustrating their use is to consider roasting turkeys. If two geometrically similar turkeys at initial temperature T0 are cooked at a given surface temperature T1 to the same dimensionless temperature distribution, then the dimensionless time, or Fourier number, with d the ‘characteristic’ diameter of a turkey, will be the same for both turkeys (if some ‘reasonable’ assumptions are fulfilled). This is the basis of roasting instructions for turkeys in cookery books and in the programming of modern ovens. Because of the temperature dependence of substance properties like density, r, or viscosity, h, to achieve thermal similarity is more difficult than to achieve kinematic similarity. Comparison across different media is only possible if the physical characteristics of the two media have a similar temperature dependence.
Historically, similarity considerations and dimensionless numbers used in modeling engineering applications are closely tied to the method of dimensional analysis. Using dimensional analysis, systems or devices can be reasoned about without explicit knowledge of the regularities that govern them (the ‘laws’ that allegedly apply to the system or device), requiring only knowledge of the relevant variables and their dimensional representation. Of course knowledge of the relevant variables will often be based on knowing (or guessing) which phenomenological equations or mechanisms will play a role in the problem at hand. Although dimensional analysis is now used much less in chemical engineering than a few decades ago, it is of (historical) interest because it involves a large number of intercalated models or ceteris paribus assumptions from the most ‘fundamental’ to the most ‘applied’. Moreover, though the number of models for which numerical solutions of the (allegedly) governing equations under the prevailing boundary conditions can be given has increased substantially, this does not mean that dimensionless numbers are disappearing from chemical engineering science and practice. In fact, new dimensionless numbers are still being added. For example, the (dimensionless) agitation cavitation number (for multiple-impeller stirred tank reactors with boiling liquids) was introduced in the 1990s. Let me give two more detailed examples, from recent issues of The Canadian Journal of Chemical Engineering, of the use of dimensionless numbers and how they are tied in with model considerations.
Liu, Fryer, and Pain (1999) consider the "influence of particle-specific gravity and particle shape on the averaged axial velocity of nearly neutrally buoyant particles in horizontal pipes". This is a problem situated in the context of modeling two phase flow (such as hydraulic transport of particulate solids). Note that the quotation (actually the title of their article) already stipulates restriction to a model. They attempt to overcome limitations of earlier purely empirical work by setting-up a proper force-balance model for the system (taking into account both particle specific gravity and particle shape). However, the equation they derive between the average particle velocity and the modified particle Froude number still contains two constants which had to be determined by regression "based on all the over 500 acquired experimental data". Moreover they can only provide approximate numerical solutions for spherical, cylindrical, disk and cubic particles, i.e. for models of actual particles, characterized using a shape factor. Finally, they list several parameters that should be included in a fuller description. After having advocated that models for the curve fitting constants in their equations should be investigated, the last sentence of their article is: "The study of single particles could be a first step towards investigations of multiple particle flows for industrial use."
Wang et al. (1999) use a multiple linear regression technique to model the airside performance of herringbone fin-and-tube heat exchangers in wet conditions. They present their results in terms of the Colburn j and Fanning friction factors (see Table 1 for these dimensionless numbers). The performance of the (highly streamlined) geometry is so complex that no single equation can describe the dependence of the heat transfer and friction on the Reynolds number and the eight parameters characterizing the geometry of the system. The curve-fitted correlation for the friction factor contains four constants, six dimensionless numbers, and five variables. The latter are powers of dimensionless numbers, all of which depend on the Reynolds number in complex ways: equations with up to four terms, containing natural logarithms in various places, several occurrences of the Reynolds number, as well as dimensionless numbers characterizing the geometry of the system.
In the sections that follow, I have restricted myself to the minimum
number of variables. This means that occasionally my equations look slightly
different from those in practice. For example, instead of the kinematic
viscosity, I write r/h.
This is innocent. Other simplifications are more problematic. Tricky variables
I use include, D, the coefficient for molecular diffusion. It is
not only dependent on the temperature, but, depending how it is defined,
depends on the bulk density and the concentration of the components (which
again can be defined in various ways). In addition, I exclude specifications
of how to evaluate substance properties (different definitions of averages,
‘bulk’, ‘at the film temperature’), various ways of defining the velocity
(‘average’, ‘bulk’, ‘film’, ‘at infinity’, ‘approach velocity’), or different
ways of taking into account a temperature gradient. Note that each of these
specifications exemplify the ubiquity of models and ceteris paribus
conditions.
Between 1890 and 1920 the ‘method of dimension’ or the ‘procedure of dimensional analysis’ was further developed. In its ‘final’ form it can be summarized according to the following steps (Bridgman 1931, Palacios 1964):
| F (P1, P2, P3, …) = 0 | (1) |
where P1, P2, P3, … represent the dimensionless groups of variables – hence called the ‘P-theorem’. Dimensional analysis does not indicate extraneous, omitted, or redundant variables (though it may offer some hints as to errors in reasoning). It only works if based on thorough familiarity with the relevant parameters. In general and often in practice there are so many Ps influencing a phenomenon that it is impossible to satisfy all the requirements of similarity at the same time – unless, contrary to one’s aims, the systems being compared are completely identical. Hence choosing a limited number of Ps involves choosing a ceteris paribus model.
Buckingham popularized the method in the United States and his name is usually associated with the P-theorem, though it was already derived by Vaschy in 1892. At the beginning of the 20th century, many physicists and engineers were implicitly using it. The subject was more or less consolidated by Bridgman (1931), in a series of five lectures presented at Harvard University.
Attempts have been made occasionally to apply dimensional analysis in
social sciences, but with little success. As Bridgman pointed out, dimensional
analysis can only be applied reliably to systems whose ‘fundamental’ laws
have been formulated. If there are as many dimensional variables as system
‘constants’ (the typical situation in social science), dimensional analysis
has no information to give.
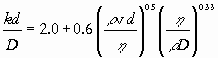 |
(2) |
There are different ways to obtain the form of correlations such as Eq. (2): [i] by dimensional analysis, [ii] by ‘un-dimensionalizing’ the differential equations for heat, mass, and momentum transfer within the boundary layers, and [iii] by listing the transport mechanisms involved – if there are n mechanisms, they can be described by n-1 dimensionless numbers. Textbooks differ in the emphasis they put on these three methods and dimensional analysis in the narrow sense has been on the retreat in the past decades. However, the different methods draw on the same principles.
To see how an equation such as (2) is obtained by using dimensional analysis, consider mass transfer between a bubble or a droplet of a fluid dispersed in another fluid – for example when a fluid with density r and viscosity h is flowing with average velocity v along a droplet with diameter d and mass transfer is taking place to (or from) the bulk of the fluid from (or to) the surface of the droplet by molecular diffusion of a reactant of which the diffusion coefficient in the fluid is D.
Then it may be suggested that the partial mass transfer coefficient,
k,
is dependent solely on the parameters mentioned, or:
| k = F(v, r, h, d, D) | (3) |
Assuming further that Eq. (3) may be expressed as a power series with
a sufficient number of constants, we can write:
| k = c1 varbdcheDf + c2vgrhdihjDk + … | (4) |
The constants in Eq. (4) are dimensionless by definition; therefore,
to be dimensionally consistent, each term in the series must have the same
dimensions as the term on the left side of the equation. In order for the
dimensions to be homogeneous, the following equations apply to the exponents
(for the three dimensions length, time, and mass respectively):
| + 1 – a + 3b – c + e – 2f = 0 | (5) | |
| – 1 + a + e + f = 0 | (6) | |
| – b – e = 0 | (7) |
Since there are three equations and five unknowns, we obtain
| k = c1 (v)a (r)a-1+f (d)a-1 (h)1-a-f (D)f | (8) |
or, by rearranging the variables into dimensionless numbers:
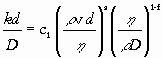 |
(9) |
| Sh = c1RemScn | (10) |
with Sh the Sherwood number, Re the Reynolds number, and Sc the Schmidt number. Eqs. (3) and (4) represent Step 2-4, Eqs. (5-7) and (8) Step 5 and Eq. (9) Step 6 in the ‘procedure’ of dimensional analysis (cf. Sect. 2).
Equation (9) is in a form made up of several groups of variables, each group of which is in itself dimensionless. Such dimensionless numbers (the P’s in the P-theorem) can often be read as a ratio of two transport mechanisms (cf. Table 1). The equation is a restatement of Eq. (3) with the necessary condition of dimensional consistency applied. The condition of dimensional consistency automatically brings into being a relationship among the exponents a, b, c, e, and f in Eq. (4) that must be satisfied in any dimensionally consistent equation. During the derivation, no conditions other than Eq. (4) were applied to the exponents. Therefore, after dimensional analysis, the remaining exponents may be constant or variable, real or imaginary, positive or negative and may be functions of any of the dimensionless groups in the equation.
The parameters c1, m,
and n in Eq. (10) can be evaluated only from experimental data or
may be ‘borrowed’ from related data using similarity considerations, For
example Eq. (2) written for mass transfer, actually ‘uses’ the parameters
c1,
m,
and n as determined for heat transfer:
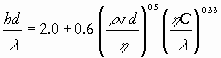 |
(11) |
or Nu = 2.0 + 0.6Re0.5Pr0.33, with Nu the Nusselt number and Pr the Prandtl number.The number 2.0 is added because for Re = 0 (no flow), theoretical analysis yields Nu = 2.0
Note that the Reynolds number occurs in both Eqs. (2) and (11); the heat transfer coefficients h and l in the Nusselt number correspond to the mass transfer coefficients k and D in the Sherwood number and similarly for the Prandtl and Schmidt number. Hence it is assumed that there is an analogy between heat and mass transfer. If the phenomenological equations for heat and mass transfer have the same mathematical form and the initial and boundary conditions are the same, then this may be the case. Because momentum transfer is vectorial, there can only be an analogy between all three transport phenomena if momentum transfer can be considered unidimensional (e.g. for momentum transfer in cylindrical tubes or along a flat plate).
Eq. (11) was obtained for a ‘simple’ geometry: a spherical droplet of
diameter d surrounded by an ‘infinitely’ extended flowing fluid.
Using ‘characteristic’ length parameters, the approach is extended to more
complex geometries, for example d being the diameter of an equivalent
sphere for packed beds or d being the film thickness for a falling
film – cf. the characteristic turkey diameter and the particle modified
Froude number mentioned in section 1.
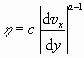 |
(12) |
The parameters c and a have to be determined for each liquid. For example (Bird, Stewart & Lightfoot 1960, p. 13), for 10% napalm in kerosene c = 0.0893 (lbfsecaft-2) and a = 0.520 (dimensionless). Though this example has been quoted from a textbook on transport phenomena of 1960, the power law for non-Newtonian fluids is still ‘the best in town’ and has not been replaced by more fundamental approaches.
A slightly different example is the ‘filtration equation’:
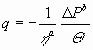 |
(13) |
with q the fluid flow per unit area, DP
the pressure difference, Q the ‘cake
resistance’ and the exponents a and b real numbers characterizing
‘the system’. The threat of ‘broken’ dimensions is easily removed in this
case, by making the variables raised to powers of real numbers dimensionless
by introducing reference values (for some standard or initial situation):
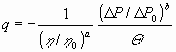 |
(14) |
Any correlation between quantified parameters can be made dimensionally invariant, even dimensionally homogeneous, by inserting enough dimensional constants, as Eqs. (13) and (14) show.
Again this example is taken from a 1960s text book of unit operations, and again the most up to date approaches to cake filtration still use power laws, though the powers have changed towards the ‘constitutional’ parameters underlying the cake resistance Q . For example, Lee et al. (2000) present a model of cake filtration that is only marginally different from models used 50 years before, though it tries to take into account the compactibility of the filter cake. Earlier approaches assume an isotropic, stationary porous matrix and Lee et al. present a model in which the latter assumption is dropped. But they still assume ‘that the gravity force and inertial terms can be neglected and that the solid particles are not deformable’. Further they assume that the porosity, e, of the cake only depends on the compression pressure and that the compactibiltiy of the cake can be described by a ‘solidosity’, 1-e , which is a smooth function of time and space. Then they can write the governing differential equations for the model. However to relate the model equations to experimental data, they still need what they call ‘constitutive equations’ for the permeability, K, and the porosity, e , for which they use power laws similar to Eq. (13). The final dimensionless equations contain five dimensionless numbers.
A second assumption underlying dimensional analysis is the choice of fundamental units (dimensions) or primary magnitudes (quantities). Table 2 is based on five ‘fundamentals’ or primary magnitudes. There is no solid justification for the choice – any number from 1 to 9 has been proposed in the context of dimensional analysis. Some say that the choice is arbitrary or depends on the particular application. Sometimes it is required that there is an operationally defined procedure of physical addition or concatenation for primary magnitudes (as in adding two masses by putting both of them in the same pan of a balance). If the latter condition does not apply, the status as primary magnitude remains disputed, temperature being the prime example. Secondary magnitudes are defined in terms of the primary magnitudes. However, there is no necessary connection between the units of derived and fundamental magnitudes and the distinction between the two is not absolute; for example, density could be made a primary magnitude. Finally, the number of fundamental units used in dimensional analysis is not necessarily the same as the minimum number of primary magnitudes to define all other physical magnitudes.
The P-theorem implies that one gets the most information out of dimensional analysis if one lists the smallest number of variables significant for the problem at hand and to have the largest number of acceptable fundamentals. Hence there have been proposals for legitimate means to increase the number of fundamentals. For example, for the flow of liquids through tubes or the flow of electricity along wires the length and the cross-sectional area can be considered independent variables and may be considered as separate ‘fundamentals’. One may also conceive of mass in two ways: related only to the inertial property of mass or to do merely with occupying space. In addition, it can sometimes be useful to regard the number of atoms as having dimensions different from a pure number. However, such choices of extra parameters are clearly guided by prior experience with the phenomena at hand.
The use of dimensionless number correlations, obtained by dimensional analysis or otherwise, further rests on the assumption that implicit functions characterizing the physical situation be complete, i.e. that all relevant dimensional system constants and variables have been listed. This involves a judgement of which parameters/mechanisms are not relevant. As an example consider some of the assumptions made in proposing an empirical correlation between the Fanning friction factor, ƒ, and the Reynolds number, Re, for flow in a cylindrical pipe:
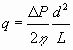 |
(15) |
This equation is valid given how the model of a cylindrical tube has been specified in the theoretical context, but numerous ceteris paribus conditions emerge if it is to be used for real world cases. Some of the ceteris paribus conditions involved in deriving the Hagen-Poiseuille equation are:
A special problem for dimensional analysis are dimensionless magnitudes,
in particular shape factors such as the ratio of the length and diameter
of a pipe, the relative roughness of a surface, the particle shape factor,
or the tortuosity of pores in a packed bed reactor. For such shape factors
there is no work to do in dimensional analysis. They occur in the list
of relevant parameters when the problem is formulated and move straight
to the resulting equation which states the relation between dimensionless
numbers. Moreover, such shape factors only take on ‘theoretical’ values
for idealized geometric models. No matter how sophisticated the theoretical
framework and no matter how powerful the numerical techniques to solve
complicated sets of differential equations, they will always apply to strongly
idealized initial and boundary conditions.
Each of the assumptions of dimensional analysis introduces its own models or ceteris paribus conditions. First, there are a number of background assumptions (models) that apply to all contexts where measurement takes place, in particular a measurement theory (consisting of axioms and operational definitions) for each of the relevant magnitudes, the choice of fundamental units, and the requirement that all equations containing magnitudes have to be dimensionally invariant. The P-theorem, which might be seen as the essence of dimensionless number modeling, draws on these background models and two more specific assumptions, which it shares with more theoretical approaches:
In the past few decades significant advances have been made toward ‘ab initio’ design in chemical engineering. Complex sets of phenomenological equations can be numerically solved for relatively complex boundary conditions. However, note that the design of equipment has gone hand in hand with finding solutions for the equations. For example, Satheesh, Chhabra and Eswaran (1999) have provided a numerical solution of the complete Navier-Stokes equations "describing the steady flow of incompressible Newtonian fluids normal to an array of long cylinders", which they say "is an idealization of many industrially important processes". There is no doubt that more often fundamental equations can be used than twenty or forty years ago, but note that [i] the solutions are numerical, not analytic, [ii] they apply to a model or idealization, [iii] which is approached in some industrial processes by making practice more streamlined.
In contrast, for real world systems, even the most ‘simple’ sort of problems remains unsolvable. Maxey Flats (Kentucky, U.S.A.) is the world’s largest commercial storage place for radioactive waste of low intensity. The management consortium said in 1963, when the site was opened, that it would take plutonium 24,000 years to get half an inch outside the borders of the site (i.e. into the soil outside the storage site). Less than ten years later, the plutonium was already two miles away from the site. In retrospect, it turned out to be impossible to make any sensible models of the boundary conditions under which the phenomenological equations concerning the relevant diffusivities and permeabilities had to be applied (Shrader-Frechette 1997). If in 1963 the solution of the complete Navier-Stokes equation "describing the steady flow of incompressible Newtonian fluids normal to an array of long cylinders" and similar ideal geometries would have been available, it would have made no difference for the prediction of possible leakage from the Maxey Flats site, because the absence of an appropriate model – no better ‘ab initio’ methods applied to simple (inappropriate) models – thwart description of the unmodeled world.
Elsewhere I have argued (van Brakel 2000), following the lead of Cartwright
(1999) and others, that all laws and models are ceteris paribus
and that the relation between a model and what it allegedly represents
is symmetrical: fitting the model is a matter of mutual attunement of both
model and reality. Cartwright has shown that the most fundamental laws
of physics only apply to model situations and are always ceteris paribus
for concrete systems. Any law or theory abstracts from ‘ordinary’ contexts;
hence it cannot be strictly true for real (actual) systems. However, phenomenological
equations too are ceteris paribus. Moreover, the example of dimensional
analysis shows that if one moves further in the direction of ‘real systems’,
the phenomenological equations take on the status of ‘fundamental theories’.
Whether there are any Newtonian fluids in the real world is an open question
and numerous other ceteris paribus conditions are introduced when
applying phenomenological equations to flow in a cylindrical tube. Moreover,
this cylindrical tube is itself an artifact. Because it has been made to
narrow specifications, phenomenological equations can be applied to it
under relatively simple boundary conditions. Both the laws or dimensionless
number correlations and the model situations to which they apply are models
because both are subject to ceteris paribus conditions. Further,
these model situations are constructed by drawing on a plethora of other
background models. What we have is a world of interrelated models, where
no matter which model or description one picks out and tries to say what
it is that is being modeled, what is being modeled is itself a model of
something else. Instead of saying that the artifact S models the given
B, it is better to say that S and B jointly make up B and S.
* This paper is a much shortened version of chapter 7 of van Brakel 2000.
Bird, R.B.; Stewart, W.E.; Lightfoot, E.N.: 1960, Transport Phenomena, Wiley, New York and London.Bridgman, P.W.: 1931, Dimensional Analysis, Harvard Univ. Pr., Cambridge/MA.
Cartwright, N.: 1999, The Dappled World: A Study of Boundaries of Science, Cambridge Univ. Pr., Cambridge.
Lee, D.J.; Ju, S.P.; Kwon, J.H.; Tiller, F.M.: 2000, ‘Filtration of highly compactible filter cake: variable internal flow rate’, American Institute of Chemical Engineers Journal, 46, 110-18.
Liu, S.; Fryer, P.J.; Pain, J.P.: 1999, ‘Influence of particle-specific gravity and particle shape on the averaged axial velocity of nearly neutrally buoyant particles in horizontal pipes’, The Canadian Journal of Chemical Engineering, 77, 1083-9.
Palacios, J.: 1964, Dimensional Analysis, Macmillan, London.
Satheesh, V.K.; Chhabra, R.P.; Eswaran, V.: 1999, ‘Steady incompressible fluid flow over a bundle of cylinders at moderate Reynolds numbers’, The Canadian Journal of Chemical Engineering, 77, 978-89.
Shrader-Frechette, K.S.: 1997, ‘Hydrogeology and framing questions having policy consequences’, Philosophy of Science, 64 (Proceedings), S149-S160.
van Brakel, J.: 2000, Philosophy of Chemistry, Leuven Univ. Pr., Leuven.
Wang, C.-C.; Du,Y.-J.; Chang, Y.-J.; Tao, W.-H.: 1999, ‘Airside performance of herringbone fin-and-tube heat exchangers in wet conditions’, The Canadian Journal of Chemical Engineering, 77, 1225-30.
Jaap van Brakel:
Institute of Philosophy, University of Leuven, Kardinaal Mercierplein 2, 3000 Leuven, Belgium; Jaap.vanBrakel@hiw.kuleuven.ac.be