 a
a  b
b 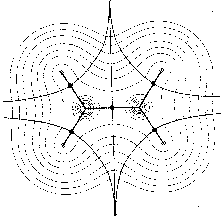 c
c
HYLE--International Journal for Philosophy of Chemistry, Vol. 3 (1997), pp. 29-49:
Dedicated to Achim Müller on the occasion of his 60th birthday
Klaus Mainzer
Abstract: Molecules have more or less symmetric and complex structures
which can be defined in the mathematical framework of topology, group theory,
dynamical systems theory, and quantum mechanics. But symmetry and complexity
are by no means only theoretical concepts of research. Modern computer
aided visualizations show real forms of matter which nevertheless depend
on the technical standards of observation, computation, and representation.
Furthermore, symmetry and complexity are fundamental interdisciplinary
concepts of research inspiring the natural sciences since the antiquity.
Keywords: molecular structure, symmetry, symmetry breaking, complexity, nonlinearity
The molecular structure hypothesis states that a molecule is a collection of atoms linked by a network of bonds. Since the 19th century the molecular structure hypothesis has been a successful concept of ordering and classifying the observations of chemistry. But this hypothesis cannot directly be derived from the physical laws governing the motions of the nuclei and electrons that make up the atoms and the bonds. It must be justified that all atoms exist in molecules as separate definable pieces of the 3-dimensional ("real") space with properties which can be predicted and computed by the laws of quantum mechanics.
The well-known models of molecules with different information for a chemist are derived from the molecular structure hypothesis: a) The three-dimensional ball-and-stick model with balls for the atomic nuclei, sticks for the atomic bonds and their angles, b) its 2-dimensional representation as structural formula, and c) its 1-dimensional representation as linguistic name which can be derived from the structural formula. Graphic models are applications of mathematical graph theory which is part of combinatorical topology. This mathematical theory became fundamental for chemistry, when in the midst of the last century the molecular structure of chemical substances were discovered (e.g., Biggs et al. 1976, p.55). L. Pasteur recognized that the relationship between symmetry of reflection and optical activity is not a function of the crystal structure of a substance. With certain water-soluble crystals, for example, the symmetry of reflection can be demonstrated both in the solid state and in the liquid state. Pasteur investigated tartaric acid and found a counterclockwise and a clockwise form, which are called L-tartaric acid and D-tartaric acid (D = dextro = right) respectively. He also isolated a third form of tartaric acid (meso-tartaric acid), which cannot be separated into one of the other forms. To explain the optical activity, it was therefore necessary to investigate more fundamental structures than crystals, or even molecules and the orientation of atoms. R.J. Haüy had already suspected that the form of crystals and their constituent components were images of one another. Pasteur therefore inferred the symmetric form of the crystal's components from the crystal reflections.
Another important step was A. Kekulé's investigation of quadrivalent carbon atoms, for whose multiple bonds he also introduced a structural formula notation which is still used in today's organic chemistry. An essential advance occurred in 1864, when the Edinburgh chemist A. Crum Brown introduced his version of the graphic notation. Each atom was shown separately, represented by a letter enclosed in a circle, and all single and multiple bonds were marked by lines joining the circles. Crum Brown's system is more or less the one in use today, except that the circles are now usually omitted. His notation was soon accepted everywhere, after some resistance from Kekulé and others. Its acceptance was partly due to its success in explaining the strange fact that there are pairs of substances which have the same chemical composition, although their physical properties are different. The graphic notation made it clear that this is because the atoms are arranged in different ways in the different substances. This well-known chemical phenomenon is called isomerism, and in many cases there are more than two isomers with the same constitutional formula. In 1874, the great British mathematician A. Cayley wrote a paper 'On the mathematical theory of isomers' inspired by the fusion of chemical and mathematical ideas.
But the experiments of J. H. van't Hoff and J. A. Le Bel were decisive for the assumption of a three-dimensional molecular structure. In 1874, independently of one another, they established a relationship between optical activity and the three-dimensional orientation of atoms. The initial example was the carbon atom, whose four valences were arranged in the form of a tetrahedron. A tetrahedral configuration with the carbon atom in the center makes possible the existence of two different arrangements being mirror images of each other. Tartaric acid has two carbon atoms which are each connected to the atoms or groups of atoms H, C, OH and COOH. For this combination, there are two possible arrangements (L- and D-tartaric acid) which are mirror images of each other and one arrangement (meso-tartaric acid) which is reflective symmetric in itself.
Van't Hoff's stereochemistry regarding the three-dimensional structure of the atom must initially have appeared to be a highly speculative idea, which betrayed a certain proximity to Platonic forms. Kekulé may have been particularly adept at three-dimensional visualization as a result of his prior study of architecture. Simultaneously with stereochemistry, geometry and algebra were also undergoing a fruitful development (Mainzer 1980, p.135). Van't Hoff's success in experimental explanation and prediction made his geometry and algebra of the molecule soon a method accepted by chemists. But it lacked any definitive physical justification. At this stage of development, stereochemistry remains a successful heuristic approach which meets chemists' need for a means by which they can visualize their structural analyses.
From an experimental point of view the shape of molecules can be illustrated by an outer envelope of their electronic charge distributions. These representations are similar to the pictures of atoms which we can today obtain experimentally by the scattering of electrons in super microscopes or from the scanning tunnelling electron microscope. It is the distribution of charge that scatters the X-rays or electrons in these experiments. Thus, it is the distribution of charge that determines the form of molecular matter in 3-dimensional space.
Mathematical methods of differential topology enable us to identify atoms in terms of the morphology of the charge distribution. The charge density r(r) is a scalar field over 3-dimensional space with a definite value at each point. Positions of extrema in the charge density with maxima, minima, or saddles where the first derivatives of r(r) vanish can be studied in the associated gradient vector field Ñr(r). Whether an extremum is a maximum or a minimum is determined by the sign of the second derivative or curvature at this point. The gradient vector field makes visible the molecular graph with a set of lines linking certain pairs of nuclei in the charge distribution.
Local maxima of electronic charge distribution are found only at the positions of nuclei. This is an observation based on experimental results obtained from X-ray diffractions and on theoretical calculations on a large number of molecular systems. Thus, a nucleus seems to have the special role of an attractor in the gradient vector field of the charge density. In short: The topology of the measurable charge density defines the corresponding molecular structure.
In the mathematical framework of dynamical systems theory the
global arrangements of molecular forces can be represented by phase portraits
with attractors as nuclei and trajectories representing the
vector field. For example, Fig. 1 shows maps with nuclei and the symmetric
structure of the ethylene molecule. In Fig. 1a only those trajectories
are shown which terminate at the position of the nuclei. They define the
basins of the nuclear attractors. Fig. 1b includes the trajectories which
terminate and originate at certain critical points (denoted by full circles)
in the charge distribution. The pair of trajectories terminating at these
critical points mark the intersection of an interatomic surface with the
plane of the figure. The gradient paths which originate at these critical
points and define the bond paths are shown by the heavy lines. Fig. 1c
shows a superposition of the trajectories associated with these critical
points on a contour map of the charge density. These trajectories define
the boundaries of the atoms in the nuclear graph.
 a
a  b
b  c
c
Figure 1: Molecular structures with nuclei as attractors in maps of the gradient vector field of their charge densities (for the plane) (Bader 1990, p. 30).
In general: the molecular graph is the network of bond paths linking pairs
of neighbouring nuclear attractors. An atom, free or bound, is defined
as the union of an attractor and its basin. Atoms, bonds, and structure
are topological consequences of a measurable molecular charge distribution.
In a next step, it is necessary to demonstrate that the topological
atom and its properties have a basis in quantum mechanics. Topological
atoms and bonds have a meaning in real three-dimensional space. But this
structure is not reflected in the properties of the abstract infinite-dimensional
Hilbert-space of the molecular state function. The state function y
contains all of the information that can be known about a nuclear quantum
system. From an operational point of view, there is too much and redundant
information in the state function because of the indistinguishability of
the electrons or because of the symmetry of their interactions. Some of
it is unnecessary as a result of the two-body nature of the Coulombic interaction.
Thus, there is a reduction of information in passing from the state function
in the infinite-dimensional Hilbert space to the charge distribution function
in the real three-dimensional space. But, on the other hand, we get a description
of the molecular structure in the observable and measurable space.
Quantum chemistry uses several mathematical procedures of approximation
to achieve this kind of reduction (e.g., Primas 1983). A well-known approximation
is the Born-Oppenheimer procedure which allows a separate consideration
of the electrons and nuclei of a molecule. We get the nuclear structure
of a molecule which is represented by its structural formula. In order
to distinguish the electrons as quasi-classical objects in orbitals, the
Hartree-Fock method is sometimes an appropriate approximation for the electronic
state function. The electronic charge density r(r,X)
with the space vector r of an electron and the collection of nuclear
coordinates X can be derived as the quantum mechanical probability
density of finding any of the electrons in a particular elemental volume.
In the case of molecules in stationary states, the probability density
is defined by the stationary-state function y(x,X)
depending on the collection x of electronic space and spin coordinates
and the collection X of nuclear coordinates (Bader 1990, p.6). This
state function is a solution of Schrödinger's stationary state equation
for a fixed arrangement of nuclei. The coincidence of the topological
definition and the quantum definition of an atom in a molecular
structure means that the topological atom is an open quantum subsystem
of the molecular quantum system, free to exchange charge and momentum with
its environment across boundaries which are defined in three-dimensional
real space. In this sense, symmetries of molecules referring to their topological
structure are real forms of matter which can be calculated by quantum chemistry.
Quantum chemistry and mathematical group theory are the modern bases of symmetry considerations in stereochemistry. In quantum chemistry the symmetries of molecular systems are represented by the symmetries of the corresponding molecular Hamiltonian operators. In stereochemistry the structure of molecules is classified by the symmetry transformations of point groups (Mainzer 1996, p. 492):
The symmetries of a free molecule can be completely defined by a few types of symmetry transformations. In general, the selection of the three coordinates axes x, y, z is arbitrary. The trivial symmetry transformation is identity I which leaves each molecule unchanged. An additional symmetry element is the axis of rotation Cn around which a molecule can be rotated by the angle 2p/n without changing its position. Linear molecules, in which all atomic nuclei lie on a straight line (e.g. nitrogen NºN or carbon monoxide CºO), can be rotated around the connecting axis by arbitrarily small angles and have a continuous axis of rotation with infinite fold symmetry n ®µ.
An additional symmetry element is the reflection s on a plane in which the molecule does not change its position. For example, if the xy-plane is the plane of reflection, then replacing all the atomic z-coordinates by -z does not change the position of the molecule. Depending on the selection of the plane of reflection, a distinction is made between a vertical plane of reflection sn and a horizontal plane of reflection sh.
The next symmetry element is inversion in which a molecule remains unchanged during a reflection of all atomic coordinates (x, y, z) at the point of inversion to (-x, -y, -z). An additional symmetry element is rotary reflection Sn = shCn in which a molecule is first rotated by an angle 2p/n around the rotary reflection axis Cn and is then reflected on the plane sh perpendicular to Cn through the centre of the molecule, without changing its position.
The remaining symmetry element is rotary inversion in which a molecule does not change its position in spite of rotation followed by inversion. It should also be noted that the compound symmetry transformations of rotary reflection and rotary inversion do not presuppose the partial transformations of rotation, reflection or inversion as symmetry elements of the same molecule. The symmetry transformations of a molecule, when executed one by one, produce symmetry transformations in turn and define as a whole the symmetry structure of the molecule by the mathematical group of these symmetry transformations.
In general, mathematical symmetries are defined by so-called automorphisms that means self-mappings of figures or structures whereby the structure remains invariant (example: rotation or reflection of polygons in the plane). The composition of automorphisms satisfies the axioms of a mathematical group. So the symmetry of a molecular structure is defined by its group of automorphisms. There are continuous groups of symmetries (for instance, circles and spirals) and discrete groups (for instance regular polygons, ornaments, Platonic bodies).
On account of the finite number of combinations of symmetry elements, it is clear that there can only be a finite number of point groups. Thereby many different molecules can belong to the same point group, i.e. they can have the same symmetry structure. The classification of point groups also makes it possible to explain the relationship of optical activity and molecular structure in terms of group theory. According to Pasteur a compound had optical activity, if the molecule in question could not be made to coincide with its reflection. In that case, Pasteur spoke of dissymmetry. Other terms are "enantiomery", which in the Greek translation means opposite shape, or "chirality", which alludes to the left and right-handedness of the reflective orientation. In terms of group theory, it is a matter of determining the elements of symmetry which lead to optical activity. In general, 1) a molecule with any axis of reflection Sn cannot be optically active, and 2) a molecule without an axis of reflection is optically active.
Point groups describe the symmetries of stationary molecules in the equilibrium state. Reduced symmetries may be present in the non-stationary case of translation, rotational motions, oscillations etc. Scalar characteristics such as mass, volume or temperature, which have only an amount but no direction, are apparently independent of the symmetry operations. But characteristics which have not only an amount but also a direction can affect the symmetry.
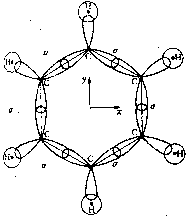
So far we have discussed the symmetries of the structures of molecular nuclei. What symmetries determine the electron orbitals of the molecules? Molecular orbitals y are frequently introduced by approximation as linear combinations of the atomic orbitals ci of the individual atoms of the molecule (Linear Combination of Atomic Orbitals = LCAO method) with y = Si ci ci . Kekulé's famous ring structure of benzene provides a clear example of orbital symmetry. The flat molecule C6H6 consists of six carbon atoms which form a regular hexagon, and each of which is bonded to a single H atom. Each carbon atom has six electrons, two of which are in closed s-shells, while the others are distributed into s and p orbitals. In Figure 2a, one valence electron of the carbon is required to bond a H atom. Two valence electrons are required for the s-bond between the carbon atoms. The s-bonds are produced by a suitable mixing ('hybridazation') of the s, px and py atomic orbitals of the carbon (Jaffé, Orchin 1967, p. 89).
 a
a  b
b
Figure 2: Orbital symmetry of Kekulé's ring structure of
benzene (Mainzer 1996, p. 498).
The fourth valence electron corresponds to the pz
orbital, which is above and below the plane with its two dumb-bells, each
perpendicular in the nodes of the carbon atom. The pz
orbitals overlap with their respective neighbors and form a p-bond.
Figure 2b shows a p-orbital of benzene. In contrast
to the s-bond, the p-bond
is weak, so that the p-electrons can be easily
influenced by extremal forces, and thus determine many of the spectroscopic
characteristics of benzene. s and p
orbitals of benzene can be distinguished by their symmetry behavior in
a reflection on the xy plane. While s orbitals
fs do not change
their sign during the reflection z ®-z and
are therefore symmetric, antisymmetry occurs with the p
orbitals fp:
fs(x,y, -z) = fs(x,y,z)
fp(x,y, -z) = -fp(x,y,z)
The system of p electrons offers a simplified way to calculate the energy levels of the benzene molecule. In the Hückel model, we first consider p-electrons, since it is assumed that p molecule orbitals are significantly higher in energy than s orbitals and can therefore be considered separately. Calculating y orbitals according to the LCAO method is therefore restricted in the Hückel model to the atomic orbitals ci which form p-molecular orbitals. That is another major simplification, of course, but one which has proven valuable in actual practice, e.g. in the calculation of benzene orbitals.
The p orbitals of benzene are eigenfunctions of a Hamilton operator of the p-electrons, which is invariant with respect to symmetry operations of the point group D6h of the regular hexagon with horizontal reflection sh. Physically, therefore, the potential energy of the p electrons is not changed when the benzene molecule is rotated, e.g. by 60° around the center. The Hückel model and the orbital symmetries thereby assumed are also used to predict chemical reactions, as expressed in the Woodward-Hoffmann rules. One requirement is that the orbital symmetry is conserved during reactions, i.e. the symmetry of all occupied orbitals remains unchanged during the reaction with respect to each symmetry element shared by the reacting and resulting molecules.
In contrast to low-molecular chemistry, high-molecular or macromolecular chemistry is concerned with compounds which are composed of a great many atoms, and therefore have high molecular masses. From the standpoint of symmetry, polymerizations are nothing more than polyadditions of monomers, the structural formulas of which form certain chains like those which are known from the Fries groups. These structural formulas recall the artful friezes in mosques, "structures of altogether unusual simplicity, unity and beauty" (W. Heisenberg). But with regard to the symmetries of the friezes of chemical structural formulas, we have to consider that these are only two-dimensional projections of three-dimensional structures. For crystal polymers in particular, X-ray diffraction spectra reveal stable conformations with well-defined symmetries.
The significance of macromolecules in nature becomes clear when we investigate the structure and metabolism of living organisms. For example, their high molecular masses makes it possible to construct solid and simultaneously flexible structures. On the other hand, their complex atomic structure makes it possible to regulate metabolic processes and to store information. From the standpoint of symmetry, proteins are of fundamental interest. These are macromolecules of many amino acids of 20 different types in nature. Protein analysis shows that amino acids have an antisymmetrical carbon atom and occur only in the left-handed configuration in nature. If we investigate the three-dimensional conformation of various amino acid units in the protein, we encounter a characteristic antisymmetry of the protein, in which the antisymmetry of its components is continued.
L. Pauling, who detected a spiral structure in certain crystal protein fibers, called it a-helix. The a-helix consists of 18 monomer units on 5 revolutions each, which, among other things, are stabilized by intramolecular hydrogen bonds. One of the characteristic symmetry breakings of biopolymers is therefore the fact that proteins in nature only form left-handed spirals. Of course, reflections of the protein components also occur, but they cannot be fitted into the molecular chains of proteins. Certain proteins differ from the regular helix structure. One well-known example is hemoglobin, whose stereochemical structure was reconstructed by the Nobel Prize winner M. Perutz, among others. To be precise, hemoglobin consists of a spherical protein (globin) and a complicated compound of iron (heme) which is not a protein. Hemoglobin is characterized by the double axis of rotation of its molecular chains.
X-ray crystallography now makes it possible to systematically analyze the symmetry structures of crystallized proteins and to explain them in terms of group theory. The mathematical structure of crystals is altogether independent of their physical or chemical interpretation. In biochemistry, atoms are not selected as structural units, but molecules. Since amino acids naturally occur in proteins only as left-handed configurations, certain symmetry elements of crystals which require an equal number of left-handed and right-handed configurations, such as the plane of reflection, glide reflection and center of inversion, are a priori excluded. Mathematically speaking, from the 230 possible crystal groups only the first 65 ones with intrinsic movements remain. These 65 discrete intrinsic motion space groups in which biological macromolecules such as proteins can crystallize are therefore also called "biological" space groups (Mainzer 1996, p.507). They are used in the investigation of enzymes, for example.
Nucleic acids, which are primarily responsible for transmitting characteristics through generations of living organisms show also characteristic symmetry breakings. Nucleic acids are macromolecules which are formed by linear polymerization of certain units (nucleotides). According to the double helix model of J.D. Watson and F.C. Crick, the DNA molecule consists of two strands of DNA which are intertwined in a regular double helix around a common axis. The two strands are parallel, but in opposite directions. The sequence of the bases in the one strand determines the sequence in the other strand, so that an A is always opposite to a T and a G is always opposite to a C. Antisymmetry is of fundamental importance for the transmission of genetic characteristics, which can be explained on the molecular level of DNA helix.
The genetic information of an organism is encoded in its set of chromosomes (genome) in the form of DNA. The mechanism of reproduction, which makes possible a clear duplication (replication or reduplication), can be illustrated very clearly: An enzyme enables to break the hydrogen bonds separating the double helix into two strands. Each strand reproduces its exact opposite, to which it is reconnected by hydrogen bonds, thereby forming a new double helix. On account of the complementary base pair formation of A-T and C-G, which is expressed in three dimensions in the twisting of the double helix, the accuracy of the copy is guaranteed even after many reproductions. If the two strands were orientated parallel and symmetric to one another like a ladder, then the accuracy of the reproductive process would not be guaranteed, with disastrous consequences for the respective organisms. This case demonstrates that antisymmetry or parity violation can have a decisive biological function.
In general, the symmetry of reflection (inversion) means that right-handed and left-handed structures of chiral molecules can be distinguished in space. But energetically they seem to be completely equivalent. It was van't Hoff who found the geometrical explanation of chiral and optically active molecules. Mathematically we can use coordinate systems with right and left orientation to distinguish both forms of chirality. In quantum chemistry the symmetry of chirality is represented by a quantum number ('parity') with two possible values +1 for positive parity and -1 for negative parity.
But the symmetry of chirality is violated by observations and measurements in the laboratories of biochemists. Macromolecules like, for instance, L-amino acids or D-sugars which are building blocks of living systems possess a characteristic homochirality or dissymmetry. Sometimes enantiomers (i.e. the reflections of isomers) can be distinguished by simple tests of taste: S-asparagin has a bitter taste, while R-asparagin has a sweet taste. We can perceive this kind of symmetry breaking, because our body is a handed (chiral) biochemical system. In the 19th century Pasteur already presumed that living systems are characterized by typical dissymmetries of their molecular building blocks which have emerged during biological evolution (e.g., Pasteur 1861). Then the handed receptor molecules of our taste organs fit the chiral forms of the tasted molecules such as the right or left hand fits the right or left glove. But it cannot be explained why the actual molecular form of symmetry breaking was realized during the evolution and why the other form was unable to survive.
As usual in classical physics, the two stable enantiomers can be illustrated by two minima of a symmetric potential curve V(q) where q is the reaction coordinate for the chemical transformation of the molecular substituents. Mathematically the potential curve of the reaction equation is assumed to be completely symmetric with respect to inversion. There are three solutions as equilibrium points with the two stable minima of the left- and right-handed forms and an unstable solution of a symmetric achiral form. The symmetry is broken by the actually realized stable form with respect to peculiar supplementary conditions.
In quantum chemistry the framework of classical physics must be replaced by the principles of quantum mechanics. Molecular states are described by wave functions which can be superposed as pure entangled states according to the superposition principle. Thus for every temperature and energy there is not only the possibility of chiral molecules with either a left- or a right-handed form, but also a third possible form which is both left- and right-handed. Spontaneous symmetry breaking in quantum chemistry can be introduced by superselection rules forbidding the symmetric achiral superposition states which can be realized by a special physico-chemical environment (e.g. certain radiation fields).
The classical and quantum mechanical concept of spontaneous symmetry breaking can only explain that a chiral molecule must emerge under some supplementary conditions. But it cannot explain why the actual form was realized instead of the other possibility. An explanation has been suggested with respect to the parity violating weak interaction which can be evaluated at least numerically in chiral molecules. In case of parity (P)-symmetry the right- and left-handed forms would be energetically exactly equivalent, transformed into each other by inversion. But parity was violated by the symmetry breaking of weak interaction during the cosmic evolution. Thus, if the parity violation can be measured by a small energy difference DEPV, we get the non-equivalence of the two isomers or enantiomers which are no longer simple mirror images of each other. The corresponding potential curve is no longer symmetric, but the two minima differ with the energy difference DEPV. Obviously the chemical law itself is no longer symmetric (Quack 1993, p. 469). Then the actually realized forms of chiral biomolecules can be explained by their greater stability with respect to the parity violating energy. The emergence of a chemical phenomenon is reduced to a physical symmetry breaking.
Of course, these energy differences in molecules are extremely small. Even if these differences increase proportionally during polymerization, they still remain very small under laboratory conditions. But in evolution, nature itself was the laboratory. For amino acids, for example, we can accurately calculate the prebiotic evolutionary conditions in which homochirality can be selected, e.g. in a lake with a certain volume of water and over a certain period of time. These calculations are based on an ab initio method (Hartree method) of numerical quantum chemistry, which currently has the best claim to accuracy. Therefore homochiral biochemistry can be interpreted as a direct result of the parity violation of weak interaction.
Pasteur's suspicion of a universal dissymmetrical force in nature is therefore reasonable, at least in terms of quantum chemistry. We could go even further and classify the chirality of biomolecules in a sequence of symmetry breakings which took place in the cosmological growth of the universe. Elementary particle physics intends to unify all the known physical interactions by deriving them from one interaction scheme based on a single symmetry group. Physicists expect to arrive at the actually observed and measured symmetries of fundamental forces and their elementary particles of interaction by spontaneous symmetry breaking processes. Electromagnetic and weak forces could already be unified by very high energies in the laboratories of high energy physics (for instance the accelerator ring of CERN). That means that at a state of very high energy the particles of weak interaction (electrons, neutrinos, etc.) and electromagnetic interaction cannot be distinguished any longer. They can be described by the same symmetry group U(1) x SU(2). At a particular critical value of lower energy the symmetry breaks down in two partial symmetries U(1) and SU(2) corresponding to the electromagnetic and weak force.
The most successful method to achieve this kind of spontaneous symmetry breaking is provided by the Higgs' mechanism. After the successful unification of electromagnetic and weak interaction physicists try to achieve the big unification of electromagnetic, weak and strong forces (GUT), and in a last step the superunification of all four forces. There are several research programs of superunifications such as supergravity and superstring theory. Technically the unification steps should be achieved along growing values of very high energy. Mathematically they are described by extension to richer structures of symmetry (gauge groups). On the other hand, the variety of elementary particles is actualized by spontaneous symmetry breaking. The emergence of weak interaction with its particular violation of parity was a result of cosmic symmetry breaking during the expansion of the universe. "C'est la dissymétrie qui crée le phénomène”, said Pierre Curie (Curie 1894).
Besides spatial symmetries chemists are involved in the fundamental problems of time symmetry. While the laws of classical physics and quantum chemistry assume symmetry with respect of time inversion, the factual chemical reactions in the laboratories proceed only in one direction to the chemical equilibrium. Chemical processes are irreversible. Their reversion seems to be unnatural. It is a question of current research, if the violation of time inversion can be experimentally observed for isolated quantum systems in analogy to the parity violation of isolated chiral molecules.
Since Boltzmann's statistical interpretation of the 2nd law of thermodynamics, irreversible processes have been discussed for complex molecular systems like gases, fluids, etc. The 2nd law states that closed systems irreversibly approach the thermal equilibrium of maximal entropy. It is remarkable that I. Prigogine explains the irreversibility of dissipative processes far from thermal equilibrium by a universal symmetry breaking of time. Time has now the status of a mathematical operator which only allows physically asymmetric states. While the spontaneous symmetry breaking of elementary particles in high energy physics assumes the symmetry of its laws with respect to unitary (gauge) groups, Prigogine's time operator delivers (non-unitary) semi-groups representing both directions of time (Nicolis, Prigogine 1989). The 2nd law of thermodynamics is a kind of selection principle for the realized symmetry breaking process. In short: The law itself has become asymmetric.
The emergence of dissipative structures far from thermal equilibrium is an irreversible process of symmetry breaking which can be geometrically illustrated by a bifurcation scheme (Mainzer 1997). In other words: The bifurcation tree of a dissipative system represents the growth of forms in an irreversible time direction. Chemical reactions provide paradigmatic cases of complex dissipative systems. In the Belousov-Zhabotinsky reaction, for instance, the forms of concentric rings or moving spirals appear when specific chemicals are poured together at a critical value. The competition of separated ring waves shows the nonlinearity of these phenomena very clearly, because in cases of a superposition or linearity the ring waves would penetrate each other like optical waves. The BZ-reaction is not only an example of a time symmetry breaking process, but a space symmetry breaking, too. The kinetic laws of chemical reactions in a (in principle unlimited) medium are invariant with respect to the group of all translations, rotations, and reflections.
In the framework of dynamical systems theory, this kind of space and time symmetry breaking refers to phase transitions of complex open (dissipative) systems far from thermal equilibrium. Macroscopic patterns ('attractors') arise from the nonlinear interactions of microscopic elements (i.e. atoms, molecules) when the energetic and material interaction of the dissipative (open) system with its environment reaches some critical value ('dissipative self-organization'). Phase transitions of closed systems near to thermal equilibrium are called conservative self-organization creating ordered structures with low energy at low temperature. A physical example of conservative self-organization is provided by a ferromagnet consisting of very many atomic elementary magnets. At a temperature T greater than a critical value Tc , these magnets point to random directions. When T is lowered, suddenly at T = Tc , a macroscopic number of these elementary magnets become aligned. The ferromagnet undergoes a spontaneous magnetization. In Landau's theory of phase transition, the average distribution of upwards and downwards pointing (average magnetization) is the order parameter of the complex system whose temporal dynamics can also be modelled by the spontaneous symmetry breaking of a bifurcation schema. Another example is the growth of crystals by annealing the system to a critical value of temperature.
In supramolecular chemistry, conservative self-organization plays a tremendous role (Müller et al. 1996). In this case molecular self-organization means the spontaneous association of molecules under equilibrium conditions into stable and structurally well- defined aggregates with dimensions of 1-100 nanometers (1 nm = 10-9 m = 10 Å). Nanostructures may be considered as small, familiar, or large, depending on the view point of the disciplines concerned. To chemists, nanostructures are molecular assemblies of atoms numbering from 103 to 109 and of molecular weights of 104 to 1010 daltons. Thus, they are chemically large supramolecules. To molecular biologists, nanostructures have the size of familiar objects from proteins to viruses and cellular organelles. But to material scientists and electrical engineers, nanostructures are the current limit of microfabrication and thus are rather small.
Nanostructures are complex systems which evidently lie at the interface between solid-state physics, supramolecular chemistry, and molecular biology (Mainzer et al. 1997). It follows that the exploration of nanostructures may provide hints about both the emergence of life and the fabrication of new materials. But engineering of nanostructures cannot be mastered in the traditional way of mechanical construction. There are no man-made tools or machines for putting together their building blocks like the elements of a clock, motor, or computer chip. Thus, we must understand the principles of self-organization which are used by nanostructures in nature. Then, we only need to arrange the appropriate constraints under which the atomic elements of nanostructures associate themselves in a spontaneous self-construction: The elements adjust their own positions to reach a thermodynamic minimum without any manipulation by a human engineer.
Historically, the idea of supramolecular interactions dates back to the famous metaphor of Emil Fischer (1894), who described a selective interaction of molecules as the lock and key principle. Today, supramolecular chemistry has by far surpassed its original focus. Molecular self-assemblies combine several features of covalent and non-covalent synthesis to make large and structurally well-defined assemblies of atoms. Single van der Waals interactions and hydrogen bonds are weak relative to typical covalent bonds and comparable to thermal energies. Therefore, many of these weak non-covalent interactions are necessary in order to achieve molecular stability in self-assembled aggregates. In biology, there are many complex systems of nanoscale structures such as proteins and viruses which are formed by self-assembly. Living systems sum up many weak interactions between chemical entities to make large ones. How can one make structures of the size and complexity of biological structures, but without using biological catalysts or the informational devices coded in genes?
Many non-biological systems also display self-organizing behavior and furthermore provide examples of useful interactions. Molecular crystals are self-organizing structures. Liquid crystals are self-organized phases intermediates between crystals and liquids with regard to order. Micelles, emulsions, and lipids display a broad variety of self-organizing behavior. An example is the generation of cascade polymers yielding molecular bifurcational superstructures of fractal order. Their synthesis is based on the architectural design of trees. Thus, these supramolecules are called dendrimers (from the Greek word dendron for tree and polymer). The construction of dendrimers can follow two basically different procedures. Divergent construction begins at the core and builds outward via an increasing number of repeating bifurcations. Convergent construction begins at the periphery and builds inward via a constant number of transformations. The former displaces the chemical reaction centers from the center to the periphery, generating a network of bifurcating branches around the center. The bifurcations increase exponentially up to a critical state of maximal size. They yield fractal structures such as molecular sponges which can absorb smaller molecules, which can then be dispersed in a controlled way, e.g. for medical applications.
Examples of cave-like supramolecules are the Buckminsterfullerenes, forming great balls of carbon atoms. The stability of these complex clusters is supported by their high geometric symmetry. The Buckminsterfullerenes are named after the geodesic networks of ball-like halls which were constructed by the American architect Richard Buckminster Fuller (1895-1983). The cluster C60 of 60 carbon atoms has a highly Platonic symmetry of atomic pentagons forming a completely closed spheroid.
Cave-like supramolecules can be arranged using chemical templates and matrices to produce complex molecular structures. Several giant clusters comparable in size to small proteins have been obtained by self-assembly. Figure 3 shows a ball-and-stick model of the largest discrete cluster (700 heavy atoms) ever characterized by X-ray structure analysis. This cluster containing 154 molybdenum, 532 oxygen, and 14 nitrogen atoms has a relative molecular mass of about 24 000. The highly symmetric "big wheel" was synthesized by Achim Müller and co-workers (Müller et al. 1995). Giant clusters may have exceptional novel structural and electronic properties: There are planes of different magnetization which are typical for special solid-state structures and of great significance for material sciences. A remarkable structural property is the nanometer-sized cavity inside the giant cluster. The use of templates and the selection of appropriate molecular arrangements may well remind us of Fischer's lock and key principle.
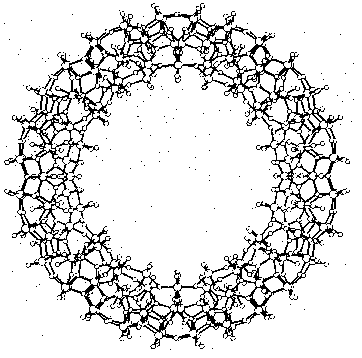
Figure 3: Supramolecular cluster in a ball-and-stick representation as an example of a complex near-equilibrium system (Müller 1995, p.2293)
Molecular cavities can be used as containers for other chemicals or even
for medicaments which need to be transported within the human organism.
An iron-storage protein that occurs in many higher organisms is ferritin.
It is an unusual host-guest system consisting of an organic host (an aprotein)
and a variable inorganic guest (an iron core). Depending on the external
demand, iron can either be removed from this system or incorporated into
it. Complex chemical aggregates like polyoxometalates are frequently discovered
to be based upon regular convex polyhedra, such as Platonic solids. But
their collective electronic and/or magnetic properties cannot be deduced
from the known properties of these building blocks. According to the catch-phrase
"from molecules to materials” supramolecular chemistry
applies the "blue-prints" of conservative self-organization
to build up complex materials on the nanometer scale with novel catalytic,
electronic, electrochemical, optical, magnetic and photochemical properties.
Multi-property materials are extremely interesting.
The growth of modern natural science is characterized by increasing mathematization and computerization. After physics in the 17th and 18th century, chemistry has been involved in that process at the latest since the 19th century. In a famous quotation Kant (1786) stated that without mathematical laws chemistry could only be a collection of experimental rules ('Experimentallehre') and no science ('Wissenschaft'). Since Kant's time the degree of mathematization in chemistry has completely changed. But there is not only an application of mathematical methods which are well-known from physics. Specific topics of chemical research has been developed with specific mathematical methods and models.
In the first chapter, I started with molecular models as typical topics of chemical research and applications of mathematical graph theory since the 19th century. A physical justification of molecular models is suggested in quantum chemistry. Furthermore, quantum chemistry provides computational procedures for chemical features which are correlated to specific molecular structures. Symmetry, dissymmetry and asymmetry are essential properties of molecular structures which are analyzed in mathematical group theory. The formation of very complex molecular systems has tremendous importance for biochemistry with the exploration of living processes and for supramolecular chemistry with the technical development of new materials. These phase transitions can be modelled in the theory of complex dynamical systems, which is a rapidly growing discipline of modern mathematics. The mathematical topology of molecular structures allows algorithmic procedures to compute correlated chemical features. But modern computer science does not only provide increasing capacities of computation, but also new insights of chemical research. Computer aided molecular design, for example, is a technique that enables chemists to simulate the structure, behavior, and interactions of molecules on computers, in order to design new drugs, chemicals, and materials such as plastics and ceramics and to test them in computer experiments.
Molecular models are typical topics of chemical research and applications of combinatorical topology and graph theory in mathematics. They correspond to, what I call, the 'structural view' of modern mathematics. Topology and group theory are typical mathematical disciplines which allow to classify molecular structures and their correlated chemical properties (e.g., symmetries of crystals, chirality of biomolecules, topological indices).
Chemistry does not only explore static structures, but dynamic processes like chemical reactions as applications of kinetic equations. They correspond to what I call the 'dynamical view' of applied mathematics. In complex molecular systems chemical interactions may be highly nonlinear and need very sophisticated mathematical instruments such as the theory of complex dynamical systems, bifurcation and chaos theory, or fractal geometry. Their application indicates a clear tendency of research from the chemistry of molecules to a chemistry of complex molecular systems. At the frontiers of modern chemistry to biology, medicine, and material sciences the dynamics of complex molecular systems plays a dominant role.
The prediction or determination of chemical events and properties needs highly developed computational procedures of numerical mathematics, approximation and algorithmic theory. Remember the ab initio computations in quantum chemistry. Theses applications correspond to, what I call, the 'numerical view' of applied mathematics. Today, the numerical procedures become more and more efficient by the increasing capacities of computer technology, for example, the power of massively parallel computers.
However, chemistry is not only interested in numerical procedures, but also in the construction of three-dimensional geometric models and the derivations of linguistic terms such as chemical formulas. Today, these activities can be assisted and even simulated by knowledge based expert systems, three-dimensional computer aided molecular design (CAMD)-programs and computer aided knowledge processing of AI-programs. Models, structures, dynamical equations, numerical, graphical and symbolic processing are combined and converted to computer programs. I call this aspect of modern computer mathematics the 'program view'. There is a clear tendency of research in all natural sciences that the traditional experiment in the laboratory is assisted by computer experiments. They are not only supplementary visualization. Their programs provide strategies to refine scientific conceptions and to focus the research in a productive manner. They help to prevent and to select less productive, expensive, or even dangerous experiments in the laboratory. But, of course, research cannot do without lab experiments, inspiring and confirming research.
The epistemic perspectives of the structural, dynamical, numerical, and program view demonstrate some typical topics of chemical research. Furthermore, they indicate changing research tendencies. Frontiers between the disciplines are removed or even broken down and new topics emerge. Chemistry is involved in a growing network of mathematical methodologies and computer-assisted technologies with increasing complexity. Thus, chemistry is a science in the sense of Kant, but with dynamically changing frontiers.
But molecular symmetry and complexity are by no means only theoretical concepts of mathematical methodology. Since the antiquity the structure of matter and the whole universe was represented by regular and symmetric models. In Platonic chemistry the variety of mathematical phenomena were reduced to the regular bodies of Euclidean symmetry. In Greek astronomy celestial movements were described by models of rational symmetry. Since the 19th century symmetries are not only defined as properties of geometric models, but as properties of physical and chemical structures, too. In this sense, symmetry means the invariance of a chemical structure with respect to spatial or time coordinates. The growths of new complex chemical structures can be understood as phase transitions close to or far from thermal equilibrium which often means symmetry breaking of spatial or time order.
In this sense, symmetry and complexity are fundamental
concepts of chemical research which refer to observable and measurable
features of matter. They are by no means only models in the head of a human
chemist or in the virtual reality of a computer. The symmetries or dissymmetries
of complex atomic structures obtained experimentally by the scattering
of electrons in super microscopes or from the scanning tunnelling electron
microscope can be observed by everyone. As once the Aristotelian opponents
of Galileo, one could object that there might be only some effects in the
measuring instruments causing our impressions. Of course, our knowledge
of molecular structures depends on our technical standards of measurement,
observation and theoretical representation. In the case of molecular structures,
these effects are well-known. Thus, molecular structures are as real as
Galileo's craters on the moon. In the antique-medieval philosophy of 'hyle',
we can summarize these results of modern chemistry in the following way:
Forms, more or less symmetric and complex, are 'in
rebus', although we can only construct representations 'in mente'.
Bader, R.F.W.: 1990, Atoms in Molecules. A Quantum Theory, Clarendon Press, Oxford.
Biggs, N.L.; Lloyd, E.K.; Wilson, R.J.: 1976, Graph Theory 1736 - 1936, Clarendon, Oxford.
Curie, P.: 1894: 'Sur la Symétrie dans les phénomènes physiques', Journal de Physique (Paris), 3, 393.
Haken, H.; Mikhailov, A. (eds.): 1993, Interdisciplinary Approaches to Nonlinear Complex Systems, Springer, Berlin.
Jaffé, H.H.; Orchin, M.: 1967, Symmetrie in der Chemie. Anwendungen der Gruppentheorie auf chemische Probleme, Heidelberg.
Kant, I.: 1786: Metaphysische Anfangsgründe der Naturwissenschaft, Kants Werke (Akademie-Textausgabe) IV, de Gruyter, Berlin 1968, p. 470.
Mainzer, K.: 1980, Geschichte der Geometrie, B. I. Wissenschaftsverlag, Mannheim.
Mainzer, K.: 1988, 'Symmetries in Nature', Chimia, 42 (5), 161-171.
Mainzer, K.: 1996, Symmetries of Nature, de Gruyter, Berlin (German edition: 1988).
Mainzer, K.: 1997, Thinking in Complexity, 3rd ed., Springer, Berlin.
Mainzer, K.; Müller, A.; Saltzer, W.G. (eds.): 1997, From Simplicity to Complexity: Information, Interaction, and Emergence, Part II, Vieweg, Braunschweig.
Müller, A. et al.: 1995, '[Mo154(NO)14O420(OH)28(H2O)70](25±5) - : ein wasserlösliches Riesenrad mit mehr als 700 Atomen und einer relativen Molekülmasse von ca. 24000', Angewandte Chemie, 107, 2293-2295.
Müller, A.; Dress, A.; Vögtle, F. (eds.): 1996, From Simplicity to Complexity in Chemistry - and Beyond, Part I, Vieweg, Braunschweig.
Nicolis, G.; Prigogine, I.: 1989, Exploring Complexity, Freemann, New York.
Pasteur, L.: 1861, Leçons sur la dissymétrie moléculaire, Paris.
Primas, H.: 1983, Chemistry, Quantum Mechanics and Reductionism, 2nd ed., Springer, Berlin.
Quack, M.: 1993, 'Die Symmetrie von Zeit und Raum und ihre Verletzung in molekularen Prozessen', Akademie der Wissenschaften (Berlin) Jahrbuch 1990 - 1992, de Gruyter, Berlin, p. 469.
Thom, R.: 1975, Structural Stability and Morphogenesis, Benjamin,
Reading MA.
Copyright Ó1997 by HYLE and Klaus Mainzer