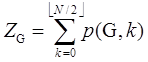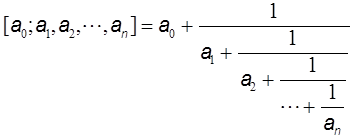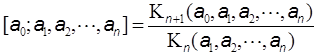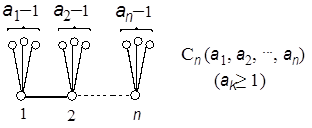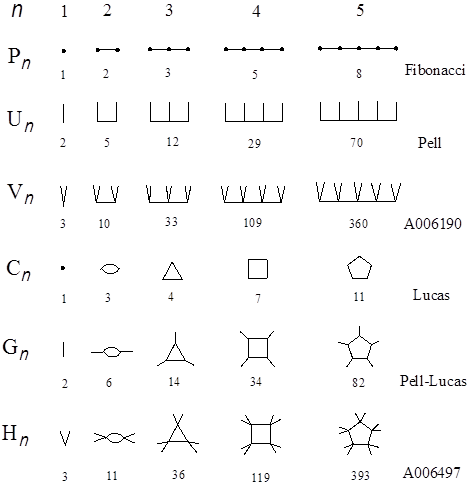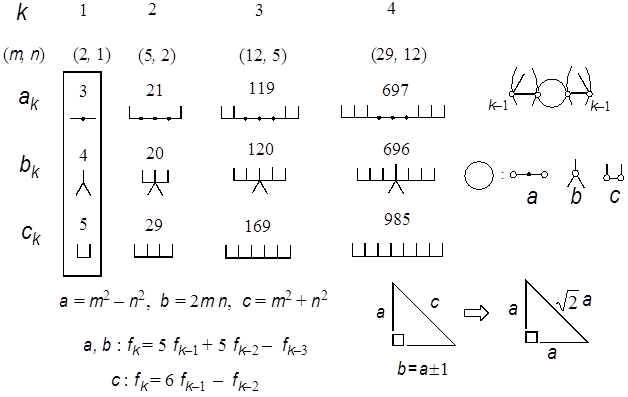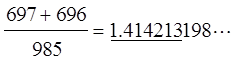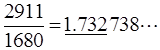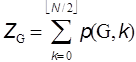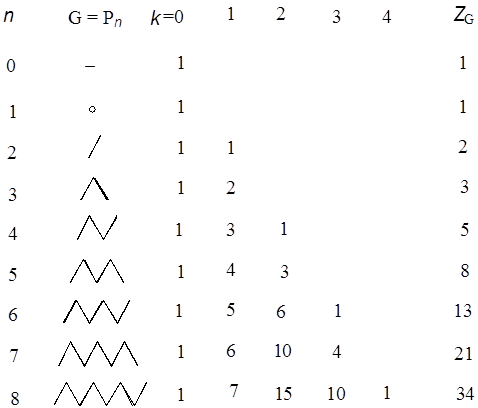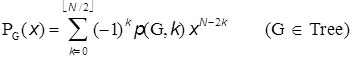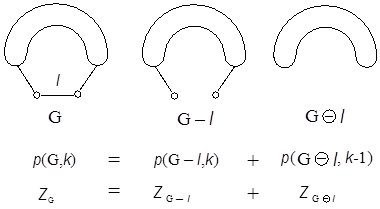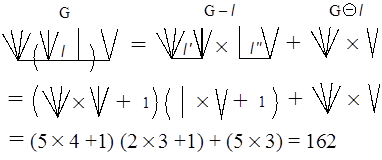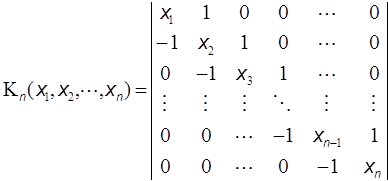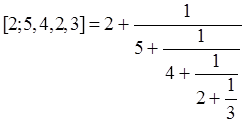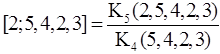What Can Mathematical Chemistry Contribute to the Development of Mathematics?

  

Abstract: It is pointed out that visualization, such as the structural formula of molecules, is the most important factor in ‘chemical thinking’. How mathematical chemistry has contributed to the development of mathematics is described with particular reference to the topological index or Z-index, proposed by the present author, and fullerene chemistry developed by mathematical chemists in various countries. Mathematical chemistry will be able to contribute to the development of mathematics by interplaying with mathematicians in the same way as it has been developing up to the present stage.

Keywords: mathematical chemistry, visualization, structural formula, graph theory, topological index, fullerene science.

 

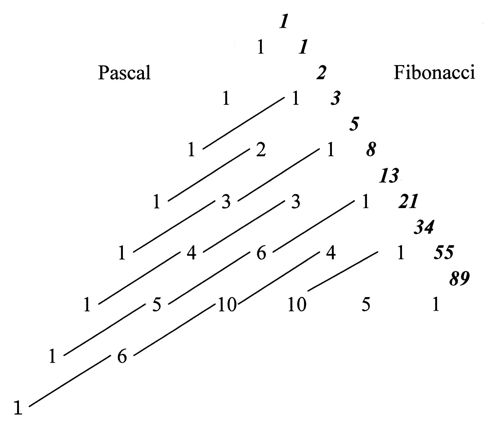
1. Introduction

The history of mathematical chemistry is indeed as short as only half a century. However, its prehistory may even go back to the era of alchemy, when people (not only alchemists themselves but also those who were surrounding and expecting them) were struggling with chaotic material to obtain pure precious substances each of which was abstracted in their brain as though mathematicians are seeking some novel abstract concept among the jungle of numbers, formulas, and their relations. This is neither an exaggerated nor an irrelevant statement.

Consider, for example, hydrogen. By looking at or by writing ‘H’, every chemist can (nowadays) routinely imagine a hydrogen atom or a mole of atomic hydrogen, although the most advanced scientific technique can never isolate or prepare any of this in a laboratory. Further, a chemist believes that a hydrogen atom is composed of a pair of electron and proton and can imagine their relative positions and movement, albeit according to Heisenberg’s uncertainty principle one cannot locate their positions and velocities simultaneously. Probably old chemists or alchemists were thinking similarly to us at the scientific level of their days.

According to the quantum theory we can obtain only the atomic wavefunction of a negatively charged light electron surrounding the proton, an extremely small particle but with heavy mass and opposite charge, either in the ground state or in some excited state. One may choose either the randomly hopping or time-averaged view of the electron by interpreting the mathematically well-defined wavefunction. From whatsoever viewpoint you have, you cannot behold the clear image of a hydrogen atom as illustrated in elementary textbooks of chemistry, even if you are allowed to creep into the subatomic world and can watch all the landscape. Nevertheless, almost all chemists can figure out the existence of a single hydrogen atom and express it by the simplest symbol ‘H’. This visualization process by chemists is not an act opposite to abstraction but can itself be considered a kind of abstraction. Visualization of chemistry-related concepts is essential in chemistry as will be clear in the following discussions.

Now go back to the H-atom. By doing the same way for other atomic species, such as C, N, O, etc., and by assigning their ‘valences’ with certain positive integers, chemists cannot only understand the structure and properties of numerous molecules each of which can be constructed from the component atoms, but also design and synthesize new substances with the structural formulas as their guiding principle (Balaban 1976).

In this way chemists can perform ‘the chemical thinking’, which was abstracted from the huge amount of information and knowledge for numerous chemical substances, such as mathematicians manipulate the way of their ‘mathematical thinking’ that was acquired from the world of numbers and beautiful logic. Thus the essence of chemical thinking and chemical logic is not so different from that of mathematical thinking (Hosoya 1981). However, the worst of it is that the majority of chemists do not know this important fact that they themselves are doing such abstraction. Then they tend to dislike and step away from mathematics.

On the other hand, mathematical chemists, who are actually a minority of all chemists, know the essence of mathematical thinking and are exploring new possibilities of applying mathematics to old and new problems in chemistry and chemistry-related fields of science. In 1971 the present author published the paper, ‘Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons’ in the Bulletin of the Chemical Society of Japan (BCSJ) (Hosoya 1971, Balaban & Ivanciuc 1999). At that time and for more than twenty years afterwards most chemists, even theoretical chemists in and outside of Japan, were skeptical of the reality of my work (Z-index for short) and mathematical chemistry as a whole (see Hosoya 2002). However, recently the mathematical essence of the Z-index was gradually recognized by mathematicians and now it is introduced in Wikipedia (2011), Wolfram’s MathWorld (2011), and other mathematical databases. The number of citations of the above paper has increased up to more than 900 now and become the second highest among all published papers in BCSJ.

With these facts as the background I will convey my thoughts on how mathematical chemistry could and will be able to contribute to the development of mathematics. As stated above, chemists like to express various concepts by using diagrams and figures as symbolized by the structural formulas of molecules. Namely, visualization is the most important execution in chemical thinking. This is quite the opposite stance by Bourbaki, a radical group of French mathematicians, which under the name of ‘New Math’ has practically overwhelmed the mathematical education systems in the world after the 1960s. Their unbelievable slogan was "Euclid Must Go kill the triangles" (Dieudonné 1959/61). Geometry-related subjects were removed from textbooks of elementary mathematics and replaced by algebra and set theory, because those geometrical objects were considered harmful to strict abstraction in mathematical thinking.

Before going into the main part of this paper the following problem needs to be pointed out: Chemists do not hesitate to use induction rather than deduction. This is quite the opposite stance of mathematicians. Although physicists may be in between chemists and mathematicians, quantum theory was actually developed by a repeated chain of induction and deduction. However, once this is established, people want to go as deductively as they can. On the other hand, a majority of mathematical chemists including myself do not stick to either stance. Just they want to solve the problem in whatever method they can choose.

2. Important role of Z-index in mathematics

In my first mathematical chemistry paper mentioned above (Hosoya 1971) a new interpretation of the mathematical relation between Pascal’s triangle and Fibonacci numbers was proposed by using the non-adjacent number, p(G,k), for the series of path graphs. Details are given in Appendix I of this paper.

See Fig. 1, where Pascal’s triangle is given with a group of slant parallel lines which give Fibonacci numbers by taking the sum of those grouped-out numbers. This fact has long been known in mathematics (Koshy 2001) but with no physical or geometrical interpretation. The new interpretation is as follows.

Consider, for example, a path graph P₆, which is obtained by joining consecutively six vertices with five edges. The non-adjacent number, p(G,k), is defined as the number of ways for choosing k disjoint edges from graph G, with p(G.0) being defined as unity for any graph. It is obvious that p(G,1) is equal to the number of edges in G, i.e., 5 in this case. The p(G,2) and p(G,3) numbers can be enumerated, respectively, as 6 and 1 as illustrated in Fig. 2.

All the remaining p(G,k)’s with k larger than 4 are zero for P₆. Since the total sum of p(G,k) for a given graph G constructed from N vertices is defined to give the Z-index as

(1)

for P₆ one gets Z_G=1+5+6+1=13, which is incidentally one of the members of the Fibonacci numbers as lined up in the right side of Fig. 1.

The reason for explaining the Z-index so deeply here is to compare this concept with Euler’s continuant (polynomial). Euler proposed the ‘continuant’ for easy manipulation of the continued fraction (see Graham et al. 1989), such as

(2)

He defined the continuant K_n(a₁, a₂,…,a_n) in a recursive way whose explanation, however, will be given also in Appendix II, and derived the relation for manipulating the continued fraction [a₀; a₁, a₂,…,a_n] as follows:

(3)

Although he could derive many useful relations for the continuant, the calculation of a given continued fraction was a little simplified, but no more than necessary.

Recently it was shown by the present author that the continuant K_n(a₁, a₂,…,a_n) is nothing else but the Z-index of the caterpillar graph C_n(a₁, a₂,…,a_n), which can be constructed by mounting the set of the star graphs X_n(a₁–1, a₂–1,…,a_n–1) onto each vertex of the path graph P_n, where a_k–1 is the number of edges of unit length emanating from the k-th vertex as seen in Fig. 3 (Hosoya 2007a).

Figure 3. Caterpillar graph.

Namely, if the Z-index of C_n(a₁, a₂,…,a_n) is denoted by Z_n(a₁, a₂,…,a_n), the above statement can be expressed as simply as

By using this relation a given continued fraction (3) can be expressed by the Z-indices of the relevant caterpillar graphs. Note that the concept of Z-index is higher than the continuant, because Z-index is defined for all the simple graphs (i.e., non-directed and without multiple edges and loops), whereas the continuant is related to only caterpillar graphs.

Since there have been known a number of useful recursive relations for enumerating the Z-index for a given graph (Hosoya 1971), Z_n(a₁, a₂,…,a_n) is easily obtained by back-of-envelope calculations. More detail explanations will be given in Appendix II.

Although details will not be given here, the solution of a linear Diophantine equation of the type

can also be solved quite efficiently by substituting this equation into the caterpillar graph expression followed by enumeration of the Z-index (Hosoya 2010). The fastest algorithm for solving the Pell equation was also obtained by using the Z-indices of caterpillar graphs (Hosoya 2007b).

Thus by using the Z-index a number of problems in elementary number theory could be solved and interpreted. Here three more examples will be shown and explained. First see Fig. 4, where six series of graphs are illustrated whose Z-indices give famous series of numbers, such as Fibonacci, Lucas, Pell, Pell-Lucas, etc. (see, for example, Weisstein 2003). All of them obey the following recursion formula,

Note that the graphs given here are the fundamental series of graphs in graph theory, such as path (P_n), comb (U_n), cycle (C_n), gear (G_n), and related graphs, while the numbers are also the fundamental series of numbers in algebra, such as Fibonacci (a=1), Pell (a=2), Lucas (a=1), Pell-Lucas (a=2), and related numbers. As is evident from Fig. 4, all these mathematical objects independently defined either in geometry or algebra could find their inherent and kindred counterparts in other fields of mathematics through the Z-index. Further, one can extend these interwoven relationships in Fig. 4 up to infinity by increasing the number of edges emanating from every vertex of the main path or cycle, and the value of a in (6), respectively, one by one.

Let us call such a graph ‘Z-graph’ whose Z-index is equal to a given Z value. Note that the Z-graph is not unique to a given graph G, because usually there exist several different G’s for a given Z. Such degeneracy increases with Z. However, for a series of graphs which are generated according to a certain rule the series of Z-graphs are sought to form regular structures as shown in Figs. 4-6.

Figure 4. Various series of graphs whose Z-indices give famous series of numbers. The alphanumerical codes are those of Sloane’s database (Sloane 2000).

By using the term Z-graph the above findings in Fig. 4 may be extended and paraphrased optimistically as follows: If a well-defined series of numbers is given, there may be a possibility of finding the corresponding series of Z-graphs with regular structure. Then why are you not optimistic about finding other beautiful examples?

Here let us see one example in Fig. 5, where trio series of Z-graphs are given to each entry of the three edges of the Pythagorean triangles with consecutive legs (Beiler 1964), such as

A Pythagorean triangle is a right-angled triangle with integer edges. Realize the rule of construction of the Z-graphs of these trio numbers. Namely, if one attaches a pair of L- and anti-L-shaped brackets to the buds (small circles given in the three graphs (a, b, c) in the right side) of the trio kernels, the Z-graphs of (3, 4, 5) framed on the left side of Fig. 5, the Z-graphs of the next larger entry (21, 20, 29) will be generated, and so on. Interestingly enough, all the Z-graphs thus generated are found to be caterpillar graphs of mirror symmetry, and we call them ‘SymCats’ (Hosoya 2009a).

As these triangles (a_k, b_k, c_k) in Fig. 5 converge to the isosceles right triangle with the increase of k, even from the data of k=4 one can obtain a fairly accurate rational number approximation of √2 as

By extending this idea one can design other series of Pythagorean triangles giving a rational number approximation of other quadratic surd, such as √3. See Fig. 6, where two trio series of Z-graphs having this property are given (Hosoya 2009b).

In this case the accuracy is not so good:

Anyway the results of Figs. 5 and 6 were obtained by a mathematical chemist as a kind of visualization of mathematics. At this stage I could not open a new field of mathematics of higher level from these findings, but I hope the box I have opened is not a kind of Pandora. The most important finding in this study is that interrelations among many different concepts originating either in algebra or geometry are established through the Z-index.

The present author believes that these success stories came from the following reason. Namely, the concept of the Z-index, although originating in mathematical chemistry, describes a geometrical or graph-theoretical concept, i.e., matching in a graph, by proper algebraic words and definitions. In other words, this is a kind of visualization process, which is very common in mathematical chemistry, applied to problems in pure mathematics, where the abstraction process prevails even over geometrical objects.

The above-mentioned Z-index matters are mere examples of the important role of mathematical chemistry for contributing to the kingdom of pure mathematics. Let us see another example, the fullerene chemistry.

Figure 6. Z-graphs of a pair of trio series of Pythagorean triangles giving rational number approximation of √3.

3. Mathematics in fullerene science

In 1985 Kroto, Smalley, Curl and coworkers first reported the discovery of C₆₀ fullerene (Kroto 1985) only from the mass spectral signals and their optimistic speculation that the soccer-ball type truncated icosahedron is the most probable structure of the C₆₀ molecule, which was later firmly proved by IR (Krätschmer et al. 1990) and NMR (Taylor et al. 1990) spectral observations. In deriving this conclusion the selection rule for these spectra played the key role by the aid of character tables for point groups of the icosahedron (I_h) and related polyhedra.

Remember that since the 1930s the quantum-mechanical theories and useful techniques using the point and rotation groups for interpreting and predicting various spectroscopic measurements of molecules were established solely by the endeavor of several talented theoretical physicists and a few chemists. This is a well-known historical fact. However, it is not widely known that even today in the curriculum of group theory taught to mathematics major students in many universities the point group is usually not included especially on its representation theory, which is the most important concept and tool for physical chemists to apply the group theory to spectroscopy.

Similarly when those fullerene scientists were struggling with C₆₀ and C₇₀, practically no helping hand was given from the mathematical side. They needed the database for the possible isomeric structures of 5,6-polyhedra of C₆₀ including other fullerenes, C_n’s, with n smaller than 100 or so, under the condition that every vertex should have three neighbors. In mathematical terminology the database they wanted to get was the complete list of all the possible cubic 5,6-polyhedral graphs with 20≤n<100 and their symmetry properties.

Of course, the famous Euler’s theorem for polyhedra,

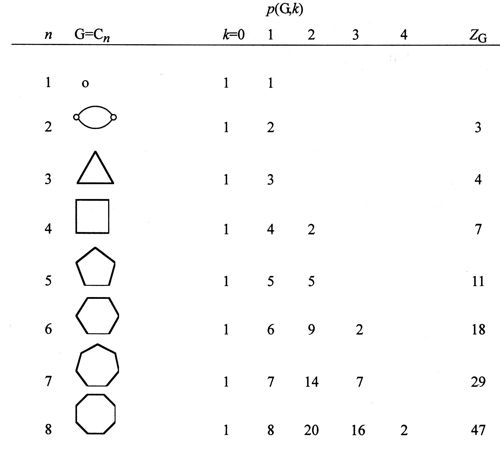
(with E being the number of edges, V the number of vertices, and F the number of faces) plays a very important role in this case, predicting that in all fullerene networks there should be 12 pentagons entangled with an arbitrary number (≥2) of hexagons.

There existed only a few partial tabulations of those polyhedra by Goldberg (Goldberg 1934, 1937). Interestingly enough, they were published in Tohoku University in Japan, which very recently suffered not a little by the big earthquake on March 11 of 2011 (but fortunately not from Tsunami and atomic power plant damage).

After several failures, three groups in the US, Great Britain, and Croatia could finally obtain the correct results for fullerene networks, which are now tabulated and available to the public (Fowler et al. 1995). For C₆₀ fullerene only the soccer-ball shaped one has such a peculiar structure among 1812 isomers that all the 12 pentagons are isolated among the sea of 20 hexagons. Such a structure with isolated pentagons was thought to be the cause of its extraordinary stability among all the isomers (Kroto 1987, Schmalz et al. 1988, Balaban & Klein 2009).

As a matter of fact all mathematically possible networks were derived from the ‘spiral algorithm’ (Manolopoulos et al. 1991) which, however, is mathematically insufficient but was later guaranteed up to several hundreds of n. On the other hand, although a mathematically rigorous algorithm by Coxeter is known, for relatively large n, it can practically be applied only to the limited number of polyhedra of high symmetry.

In the enumeration problems of discrete mathematics and practical chemistry, we often meet such a dilemma of a neat but impractical mathematical method and ‘brute force’ searching. Scientists may choose the latter stance when they are forced to choose one. Especially chemists are struggling with a melting pot of chemical substances of a huge number of species. Even though the number is huge , it is not infinite but finite. So we try to solve this practically, even if the method is not mathematically neat and complete. In many cases, however, the obtained results could be proven by mathematical induction. This problem will be discussed more deeply in the final section of this paper.

The next step to be taken for solving fullerene problems was the quantum-mechanical calculation of the electronic states of all isomers. There are two main roads for understanding and reproducing the electronic structure of molecules, i.e., molecular orbital (MO) and valence-bond (VB) methods, both of which were developed and established by theoretical physicists and chemists since 1927 (Heitler et al. 1927). The only exception was C.A. Coulson, originally a mathematician in Oxford, who not only published many key papers in this field but also mentored several brilliant theoretical chemists. In that period of time mathematical chemistry was not yet categorized in chemistry. Before computers were available to theoretical chemists, Coulson’s school was not trying to perform huge calculations but to formulate important concepts in chemistry by using beautiful mathematics. The most prominent achievement was attained by Coulson and Longuet-Higgins, who could formulate important electronic quantities defined in MO theory in terms of contour integrals over the complex plane (Coulson et al. 1947). By extending his theory I could obtain a mathematical foundation for the application of my Z-index to Hückel MO method (Hosoya et al. 1976). In this sense Coulson and Longuet-Higgins are surely the prominent ancestors of mathematical chemists.

Since there are straightforward recipes for the MO method, it was soon concluded that the soccer-ball shaped C₆₀ was the most stable and that there may be almost no chance for preparing other isomers. Due to its high symmetry the 60X60 determinant of Hückel MO was shown to be highly factorable down to the product of polynomials smaller than 3X3 by using the concept of ‘topological symmetry’ which was gained during the study of factorization of determinants (Hosoya et al. 1994).

On the other hand, from the VB side it took several years to get the number of perfect matchings, or Kekulé structures of this network to be a highly factorable number of 12500 = 2²X5⁵ (Hosoya 1986, Schmalz et al. 1986). Nowadays the number of Kekulé structures for giant fullerenes with 60n² (n=2) vertices has also been calculated (Milicevic et al. 2006). It is as large as 21,587,074,966,666,816 = 2⁶X29X269³X773². Again all these results were obtained by mathematical chemists, although the perfect matching has long been an important quantity in graph theory (for example, Harary 1969, Skiena 1990). Thus all the fullerene mathematics were obtained and established without the help of mathematicians. However, the conjecture posed by the present author (Hosoya 1986) that the perfect matching number for highly symmetrical polyhedral graph is highly factorable is not yet solved.

4. Conclusion

We have seen many different interplays of mathematical chemistry and mathematics. In some sense, mathematical chemists especially myself, are easy-going compared to the strict mathematicians, especially Bourbaki people. All our works are visualization of something and are sticking to induction rather than deduction. Some of the results obtained by us contain important information even in pure mathematics, although that does not necessarily mean that they were derived by mathematically neat methods.

Let me introduce a metaphor. Automobiles (cars) were invented to help carry people and heavy things faster and further, and nowadays many people are using their own cars for those purposes. Namely, most people drive their cars for helping themselves, and the cars are not their goal or purpose. However, it is true that there is a certain limited number of people, such as automobile makers and F1 racers including their supporting teams, to whom cars are the end of their lives and something to venture their lives for. Nobody can stop them, because they can do what other people cannot do.

On the other hand, not only mathematical chemists but also theorists in various fields of science love mathematics and they use and develop mathematics to attain their goals. Mathematics is not the property of a limited number of mathematicians who cannot survey and follow every detail of the rapid, wide, and deep development of modern science. Mathematics should be developed by humankind as was the case with the very beginning of its long history. If something happens wrong in some new mathematics, mathematicians have a right and duty to advise, correct, or improve it. Anyhow, mathematical chemistry will be able to contribute to the development of mathematics by interplaying with mathematicians in the same way as it has been developing up to the present stage as it stands now.

References

Balaban, A. T. (ed.): 1976, Chemical Applications of Graph Theory, London: Academic Press.

Balaban, A.T. & Ivanciuc, O.: 1999, ‘Historical Development of Topological Indices’, in: J. Devillers & A.T. Balaban (eds.), Topological Indices and Related Descriptors in QSAR and QSPR, Amsterdam: Gordon and Breach, pp. 21-57.

Balaban, A.T. & Klein, D.J.: 2009, ‘Claromatic Carbon Nano-Structures’, Journal of Physical Chemistry, C, 113, 19123-33.

Beiler, A.H.; 1964, ‘The Eternal Triangle’, in: Recreations in the Theory of Numbers. The Queen of Mathematics Entertains, New York: Dover, pp. 104-34.

Coulson, C.A. & Longuet-Higgins, H.C.: 1947, ‘The Electronic Structure of Conjugated Systems. I. General Theory’, Proceedings of the Royal Society London, Ser. A, 191, 39-60.

Dieudonné, J.: 1959/1961, ‘New Thinking in School Mathematics’, International Conference on Mathematics, France, Paris: OEEC, pp. 31-46.

Fowler, P.W. & Manolopoulos, D.E.: 1995, An Atlas of Fullerene, Oxford: Clarendon.

Harary, F.: 1969, Graph Theory, Reading, MS: Addison-Wesley.

Goldberg, M.: 1935, ‘Isoperimetric Problem for Polyhedra’, Tohoku Mathematical Journal, 40, 226-36.

Goldberg, M.: 1937, ‘A Class of Multi-Symmetric Polyhedra’, Tohoku Mathematical Journal, 43, 104-8.

Graham, R.L.; Knuth, D.E. & Patashnik, O.: 1989, Concrete Mathematics. A Foundation for Computer Science, Reading, MS: Addison-Wesley, pp. 287-305.

Heitler, W. & London, F.: 1927, ‘Hydrogen molecule’, Zeitschrift für Physik, 44, 455-72.

Hosoya, H.: 1971, ‘Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons’, Bulletin of the Chemical Society of Japan, 44, 2332-9.

Hosoya, H. & Hosoi, K.: 1976, ‘Topological Index as Applied to p-Electronic Systems. III. Mathematical Relations among Various Bond Orders’, Journal of Chemical Physics, 64, 1065-73.

Hosoya, H.: 1981, ‘Chemical Thinking and Mathematical Thinking – Interaction through Structural Formula’, Journal of Science Education in Japan, 5, 167-75.

Hosoya, H. & Tsukano, Y.: 1994, ‘Efficient Way for Factorizing the Characteristic Polynomial of Highly Symmetrical Graphs Such as the Buckminsterfullerene’, Fullerene Science & Technology, 2, 381-93.

Hosoya, H.: 2007a, ‘Continuant, Caterpillar, and Topological Index Z. Fastest Algorithm for Degrading the Continued Fraction’, Natural Science Report of Ochanomizu University, 58 (1), 15-28.

Hosoya, H.: 2007b, ‘Pell Equation. IV. Fastest Algorithm for Solving the Pell Equation’, Natural Science Report of Ochanomizu University, 58 (1), 29-37.

Hosoya, H.: 2009a, ‘Pythagorean Triples. III. Systematic Generation of Primitive Pythagorean Triples by the Topological Index and Caterpillar Graphs’, Natural Science Report of Ochanomizu University, 60 (1), 15-30.

Hosoya, H.; 2009b, ‘New Mathematics in Pythagorean Triangles (in Japanese)’, Sugaku Seminar, 48 (11), 49-55.

Hosoya, H.: 2010, ‘Continuant, Caterpillar, and Topological Index Z. III. Graph-theoretical Algorithm for and Interpretation of Solving Linear Diophantine Equations’, Natural Science Report of Ochanomizu University, 60 (2), 17-27.

Hosoya Index: 2011a, ‘Hosoya index’, Wikipedia [online at: http://en.wikipedia.org/wiki/Hosoya_index, accessed [March 17, 2013].

Hosoya Index: 2011b, ‘Hosoya index’, Wolfram MathWord, [online at: http://mathworld.wolfram.com/HosoyaIndex.html, accessed [June 25, 2013].

Koshy, T.: 2001, Fibonacci and Lucas Numbers with Applications, New York: Wiley, pp. 151-63.

Krätschmer, W., Fostiropoulos, K, & Huffman, D.R.: 1990, ‘The Infrared and Ultraviolet Absorption Spectra of Laboratory-Produced Carbon Dust: Evidence for the Presence of the C₆₀ Molecule’, Chemical Physics Letters, 170, 167-70.

Kroto, H.W.: 1987, ‘The Stability of the Fullerenes, C_n, with n 24, 28, 32, 36, 50, 60, and 70’, Nature, 329, 529-31.

Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F. & Smalley, R.E.: 1985, ‘C₆₀; Buckminsterfullerene’, Nature, 318, 162-3.

Manolopoulos, D.E.; May, J.C. & Down, S.E.: 1991, ‘Theoretical Studies of Fullerenes: C₃₄ to C₇₀’, Chemical Physics Letters, 181, 105-11.

Milicevic, A. & Trinajstic, N.: 2006, ‘Combinatorial Enumeration in Chemistry’, in: Chemical Modelling: Applications and Theory, vol. 4, London: Royal Society of Chemistry, pp. 405-69.

Schmalz, T.G.; Seitz, W.A.; Klein, D.J. & Hite, G.E.: 1986, ‘C₆₀ Carbon Cages’, Chemical Physics Letters, 130, 203-7.

Schmalz, T.G.; Seitz, W.A.; Klein, D.J. & Hite, G.E.: 1988, ‘Elemental Carbon Cages’, Journal of the American Chemical Society, 110, 1113-27.

Skiena, S.: 1990, Imprementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, Reading, MA: Addison Wesley.

Sloane, N.J.A.: 2000, The On-Line Encyclopedia of Integer Sequences [online at: http://www.research.att.com/~njas/sequences, accessed June 25, 2013].

Taylor, R.; Hare, J.P.; Abdul-Sada, A. & Kroto, H.: 1990, ‘Isolation, Separation and Characterisation of Fullerenes C₆₀ and C₇₀’, Journal of the Chemical Society, Chemical Communications, 1990, 1423-5.

Weisstein, E. W.: 2003, CRC Concise Encyclopedia of Mathematics, 2nd edn., Boca Raton, FL: Chapman & Hall.

Appendix: I. Topological index Z_G (Hosoya 1971)

A graph G is a mathematical object composed of vertices and edges. An edge has a pair of vertices at both ends. Here we are concerned only with those graphs which have no directed and multiple edges. First define the non-adjacent number, p(G,k), as the number of ways for choosing k disjoint edges from G (See Fig. 2). Here p(G,0) is defined to be unity for all graphs including the vacant graph f, and p(G,1) is equal to the number of edges in G. Then the topological index, or Z-index Z_G, is defined as the total sum of p(G,k)’s as

(A1)

where N is the number of vertices in G. The Z-index can be deemed as the total matchings plus one (Hosoya 1971).

In Tables A1 and A2 the p(G,k)’s and Z_G’s for the series of path graphs {P_N} and monocyclic graphs {C_N} are given. Their Z_G’s are, respectively, Fibonacci and Lucas numbers. It can be shown (Hosoya 1971) that for tree graphs (without any cycle) the characteristic polynomial P_G(x) which is defined by using the adjacency matrix A and unit matrix E as

can be expressed by the set of p(G,k)’s as in Tables A1 & A2.

(A3).

Various recursion formulas for calculating Z_G have been known. For example, see Fig. A1, where G–l and GQ l are the subgraphs of G obtained by deleting an arbitrary edge l from G, and further all the edges adjacent to l, respectively. Note that p(G–l,k) counts the l-exclusive selection of k disjoint edges, while p(GQ l,k–1) gives the l-inclusive counts for k disjoint edges. According to the inclusion-exclusion principle the sum of these two contributions gives the desired p(G,k). The recursion formula of Z_G is also given in Fig. A1.

A caterpillar graph C_n(a₁, a₂,…, a_n) has already been defined in the main text as in Fig. 3. By applying the recursion formula just introduced here to a general caterpillar graph one gets the useful recursion formula of Z_G for it, as demonstrated in Fig. A2.

See Fig. A3 for calculating the Z_G value of caterpillar graph C₄(5, 4, 2, 3), which is composed of path graph P₄ and the set of four star graphs, (S₅, S₄, S₂, S₃), or complete bipartite graphs, (K_1,4, K_1,3, K_1,1, K_1,2). Notice that the Z_G value for S_n+1 or K_1,n is n+1 since p(G,0)=1, p(G,1)=n, and p(G,k)=0 for k≥2. Then it is straightforward to get

For the later discussion, let us calculate the Z_G for C₅(2, 5, 4, 2, 3) to be 355. The readers are encouraged to get this number by themselves.

Figure A3: Calculation of Z_G value of caterpillar graph C₄(5, 4, 2, 3).

Appendix II: Continuant of Euler

The continuant polynomial was proposed to be defined recurrently by Euler as follows (Graham et al. 1989):

Among several relations for the continuant the following three will be introduced here.

1. Reversible character

(ii) Recursive relation

3. Tridiagonal determinantal expression

(A7)

Now let us evaluate the following continued fraction

according to the recipe by Euler. Namely, by using (3) one gets the following expression

The problem is now reduced to calculate the two continuants in the denominator and numerator of the right-hand-side of the above formula. Now according to (A6) we have

and

Then we get

Compare this manipulation of K’s with that of Fig. A3 at least for the numerator. Euler’s algorithm is forced to execute in one direction either from right or left. On the other hand, the algorithm for calculating Z_G is free to cut the caterpillar graph into half wherever possible and how often as you wish.

As already stated in the main text the advantage of our method comes from the fact that the concept of Z_G is higher than the continuant and moreover there are so many useful recursion relations for calculating Z_G of G for arbitrary structures.

Haruo Hosoya:
Ochanomizu University, Bunkyo-ku, Tokyo 112-8610, Japan;
hosoya.haruo@ocha.ac.jp