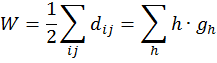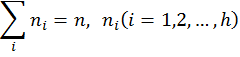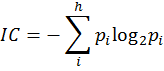Philosophy of Mathematical Chemistry: A Personal Perspective

  

Abstract: This article discusses the nature of mathematical chemistry, discrete mathematical chemistry in particular. Molecules and macromolecules can be represented by model objects using methods of discrete mathematics, e.g., graphs and matrices. Mathematical formalisms are further applied on the model objects to distill various quantitative characteristics. The end product of such an exercise can be a better understanding of chemistry, the development of quantitative scales for qualitative notions of chemistry, or an illumination of the structural basis of chemical and biological properties. The aforementioned aspects of mathematical chemistry are discussed based on my own practitioner’s perspective.

Keywords: molecular graph, mathematical chemistry, quantitative structure-activity relationship (QSARs).

 

Ostensibly there is color, ostensibly sweetness, ostensibly bitterness, actually only atoms and the void.
(Galen, after Schrödinger 1954, p. 30)

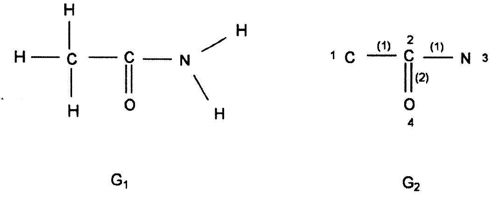
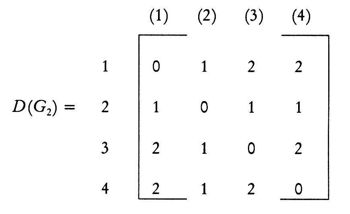
1. Introduction: A Brief History of Mathematical and Chemical Concepts

Mathematical concepts have been developed by mankind for a long time. During the period of the Rigveda (1700-1100 BC), the Hindus of the Indian subcontinent developed Vedic geometry (sulva) and astronomy (jyotisa) in an effort to guide matters of day to day necessity (Datta 2004, p. 18). Sacrifice (jajna) was the principal religious evocation at that time and each jajna had to be performed using an altar possessing a precise size and shape. This gave birth to the study of the geometrical nature of objects and resulted over time in the formulation of the science of geometry. Vedic astronomy arose out of the need of determining the proper time for religious sacrifice. Although originally required to address practical day to day problems, these sciences outgrew their original purpose and came to be cultivated by practitioners as basic research for their own sake. Sulvashastra (the science of geometry) by Baudhayana (600 BC), who was anterior to Pythagoras, seems to have the knowledge of the theorem which is now popularly attributed to Pythagoras (Datta 2004, p. 18). The development of a certain level of mathematical knowledge dictated by the material needs of the contemporary society is a common phenomenon across all civilizations (Nath & Bag 2004, p. 36). The term ganita (the science of calculation) appears frequently in the Vedic literature (Datta 2004, p. 18).

Greek mathematics would usually contain four sections: number theory, geometry, music, and astronomy. This division, the quadrivium (the ‘four ways’), lasted in the European culture until the end of the Middle Ages. One can see bas-reliefs and paintings representing the four branches of the quadrivium on the walls or pillars of cathedrals in several places in Europe (Artmann 1988, Papadopoulos 2002). Pythagoras (ca. 580-500 BC) initiated a tradition that persists to the present day – the use of mathematics in the characterization of the natural world. He and his followers are thought to be the first to conduct scientific investigations on the nature of sound. Pythagoras observed the harmony of the sound of hammers in a blacksmith’s forge, and then discovered that the weight of the hammers that produced pleasant sounds were in ratios of simple whole numbers (Caleon & Ramanathan 2008). Pythagoras and the Pythagoreans went much further, relating their notion of musical harmony to the larger order in the structure of the cosmos, believing that the arrangement of planets follows a musical progression, with the ratio of their distances also being expressible in simple whole numbers (Dampier 1961, p. 17). Pythagoreans also believed that only persons possessing special gifts could hear the ‘music of the spheres’. Incidentally, diverse mathematical concepts have been used in understanding the basis of painting (Atalay 2006, p. 26), Western music (Helmholtz 1964, p. 234) as well as the ragas of the Indian classical music (Balasubramainan 2002, Tarakeswara & Prasad 2011). The Pythagorean view is tantamount to saying that the universe is quantized (Caleon & Ramanathan 2008).

The history of the interaction between mathematics and chemistry has been reviewed by Trinajstić (1997, p. 17). Plato associated with each fundamental elements of nature (water, air, earth, and fire) a polyhedron: tetrahedron (fire), octahedron (air), hexahedron (earth), and icosahedron (water). In modern times, Cayley (1857) developed the mathematical formalism of calculating the number of possible alkane isomers having empirical formula C_nH_2n+2, and of alkyl radicals C_nH_2n+1, with the value of n ranging from 1 to 13. It was probably the first attempt of calculating the number of related substances arising out the same composition (empirical formula) using mathematical concepts. One important milestone in the early development of mathematical chemistry came from the research of Sylvester (1878, p. 64) who used the term chemicograph for what is now known as chemical graphs. Trinajstić (1997, p. 29) has pointed out that Sylvester’s work was probably ”inspired by Crum Brown’s graphic notation”. The advent of modern mathematical chemistry probably began with the seminal work of Harry Wiener (1947). For an excellent review of the major aspects of modern mathematical chemistry, see Restrepo & Villaveces 2012.

2. Mathematical Modeling of Chemical Structure: Representation and Characterization

As pointed out by Schummer (1998), one important aspect of the cognitive architecture of chemistry is the theoretical foundation through the chemical theory of structural formulas. Representation of molecules by different structural models, e.g., a graph, a stick-and-ball model, three dimensional data sets, use different theoretical frameworks to derive useful chemical information (Basak et al. 1991). In mathematical chemistry, two crucial steps are: (a) abstraction of the model object and (b) derivation of the mathematical model (Basak et al. 1991, Bunge 1973). The model object corresponding to a chemical substance represents the salient feature of its structure. The structure of an assembled entity, e.g., a molecule, is the pattern of relationships among its constituent parts. But the term ‘molecular structure’ represents a set of nonequivalent and probably disjoint concepts (Primas 1983). There is no reason to believe that when we discuss diverse topics – e.g., chemical synthesis, reaction rates, spectroscopic transitions, reaction mechanisms, and ab initio calculations – the different meanings we attach to the single term ‘molecular structure’ originate from the same fundamental concept. This has been termed "the molecular structure conundrum" (Weininger 1984). In the context of molecular science, the various representations of molecular structure, e.g., ‘classical’ valence-bond representations, various chemical graph-theoretic representations, ball and stick models, minimum energy conformations, or symbolic representation of chemical species by Hamiltonian operators, are model objects (Basak et al. 1991, Bunge 1973) derived through different abstractions from the same chemical reality. In each instance, the equivalence class (the concept or model of molecular structure) is generated by selecting certain aspects while ignoring other unique properties of those objects. This explains the plurality of the concepts of molecular structure and their autonomous nature, the word ‘autonomous’ being used in the same sense that one concept is not logically derived from the other.

3. Representation of Molecular Structure

Quantum chemistry and mathematical chemistry are two major methods of carrying out mathematical modeling on chemical structure. As is well known, for a single molecule one can use different levels of theories for quantum chemical calculations (Basak et al. 2003a,b). We will not discuss quantum chemical methods here. Instead, we will deal with concepts and methods of mathematical chemistry which deals with the representation and characterization of molecular structure using methods derived from discrete mathematics, e.g., chemical graph theory and topology (Balaban 1976, Basak & Mills 2009, Kier & Hall 1986, 1999, Trinajstić 1992).

A graph, G = [V, R], is defined as an ordered pair consisting of two sets V and R, where V represents a finite nonempty set of points, and R is a binary relation defined on the set V (Harary 1969). The elements of V are called vertices and the elements of R, also symbolized by E, are called edges. In graph theoretical models of molecular structure, i.e. molecular graphs, V represents the set of atoms and E usually depicts the collection of covalent bonds in the molecule (Trinajstić 1992). It should be noted, however, that the set E does not need to be limited to covalent bonds. Elements of E may symbolize any type of bond, viz., covalent, ionic, or hydrogen bonds, etc. It was emphasized by Basak et al. (1988a) that weighted pseudographs constitute a very versatile model for the representation of a wide range of chemical species. A molecular graph may contain either all atoms present in the empirical formula or only non-hydrogen atoms. Hydrogen-filled graphs are preferable to hydrogen-suppressed graphs when hydrogen atoms are involved in critical steric or electronic interactions. The hydrogen filled (G₁) and hydrogen-suppressed (G₂) graphs of acetamide are given in Fig. 1.

Different types of graphs can be used to represent chemical species, e.g., directed graphs, undirected graphs, linear graphs, and multigraphs. Here we consider only connected and undirected graphs to represent molecular structures. Such graphs are often called molecular graphs.

Various levels of chemical information can be coded in molecular graphs. At the most fundamental level, topostructural models contain information regarding only the connectivity of atoms without any consideration of the precise chemical nature of vertices (atoms) or edges (bonds). For example, the distance matrix, D(G₂), of the molecular graph G₂ (vide infra) represents only the pattern of connectivity of atoms in the molecule without any consideration of the type of atoms or their bonding patterns. Topochemical models of molecules, on the other hand, are weighted molecular graphs in which one assigns chemically meaningful weights to the vertices and edges (Basak et al. 1988a, 1997). For example, the electrotopological state indices (Hall 2012, Kier & Hall 1999), neighborhood complexity indices (Basak 1987), and variable connectivity indices (Randić & Basak 2001) fall in the latter category of models.

4. Characterization of Molecular Structure by Mathematical Formalisms

Molecular graphs can be represented by various types of matrices (Trinajstić 1992, Janežič et al. 2007). The adjacency and distance matrices have been used in mathematical chemistry for many purposes. The distance matrix D(G₂) for the labeled graph G₂ in Figure 1 may be written as follows:

Hosoya (1971) coined the term topological index (TI) for numerical descriptors derived from matrices of molecular structures. As shown by Hosoya, the first topological index, the Wiener index W (Wiener 1947), can be calculated from the distance matrix D(G) of a hydrogen-suppressed graph G as the sum of entries in the upper triangular submatrix:

where g_h is the number of unordered pairs of vertices whose distance is h.

A number of software is now available for the calculation of topological indices (TIs) of molecules (Basak et al. 1988b, Semichem 2012, Hall 1996, Todeschini 2004). Graph theoretical methods have been used for the characterization and discrimination of structures (Balasubramanian & Basak 1998, Randić 1984, Raychaudhury et al. 1984), the prediction of property, bioactivity, or toxicity of small molecules like drugs and environmental pollutants (Basak 2010), the characterization of macromolecular sequences like DNA (Nandy et al. 2006, Randić et al. 2000), the quantification of proteomics maps (Basak & Gute, 2008, Randić et al. 2001), the representation and mathematical characterization of proteins (Ghosh & Nandy 2011, Randić et al. 2011), the understanding of the properties of specific protein sequences related to the virulence of pandemic Bird Flu (Ghosh et al. 2009), the prediction of biochemical modes of action (MOA) of chemicals (Basak et al. 1998), the structure based clustering of large combinatorial libraries of structures (Basak et al. 2010), the mathematical characterization of chirality of molecular structures (Natarajan & Basak 2011), and understanding the structural basis of alterations in mechanisms of drug-target interaction arising out of the development of drug resistance in microbes (Basak et al. 2011), to mention just a few applications.

5. Quantification of Qualitative Chemical Concepts

Techniques of mathematical chemistry have been used to quantitatively characterize qualitative concepts like chirality, branching, complexity, etc. For chirality, readers are referred to our recent review (Natarajan & Basak 2011). Here we discuss only two additional examples of the applications of methods of mathematical chemistry in the quantification of qualitative ideas: (a) molecular branching and (b) complexity.

5.1 Molecular Branching

For many physical properties, e.g., hydrophobicity, alteration of the degree of branching in the structure brings about a definite change in the magnitude of the property. Many numerical graph invariants can be used for the quantification of branching (Bonchev & Trinajstić 1977, Randić 1975, Raychaudhury et al. 1984, Wiener 1947) because their magnitudes are sensitive to the branching patterns in the structure. One well known example of the quantification of the notion of molecular branching is Randić’s (1975) connectivity index which is an invariant defined on the simple graph (topostructural) model of alkanes.

Randić’s connectivity index, ^1 , is defined as:

The various branching indices mentioned above and many others known in the literature transform qualitative and relative notions, like ‘more or less branched’, into a quantitative numerical scale, although the numerical ordering of the same set of molecules, e.g. the group of isomeric eighteen octanes, may vary from one index to another.

5.2 Molecular Complexity

Complexity is an intrinsic property of all natural and man-made systems. Information theoretic formalisms have been used in the quantification of complexity of chemical systems as well as of networks (Bonchev 2009, p. 4820; Dehmer 2008).

The structure of an assembled entity is the pattern of relationships among its constituent parts. Another important notion regarding structure is that it presents to us a message that encodes certain amount of information (Bonchev 2009, p. 4820). In chemistry, given a set of molecules, chemists often talk about their relative complexity, which is often a qualitative idea. But various authors over the past four decades have developed quantitative measures of atomic and molecular complexity based on information theoretic invariants of graphs corresponding to them (Bonchev & Trinajstić 1977, Raychaudhury et al. 1984, Basak 1987, Bonchev 1983, 2009, p. 4820).

Information theoretic invariants are calculated by the application of information theory to chemical graphs. An appropriate set A of n elements is derived from a molecular graph G depending upon certain structural characteristics. On the basis of an equivalence relation defined on A, the set A is partitioned into disjoint subsets A_i of order n_i:

A probability distribution is then assigned to the set of equivalence classes A₁, A₂,…, A_h with p₁, p₂,…, p_h, where p_i = n_i/n is the probability that a randomly selected element of A will occur in the i^th subset.

The mean information content (IC) of an element in A is defined by Shannon’s relation (Shannon 1948, Rashevsky 1955, p. 229):

The logarithm is taken at base 2 for measuring the information content in bits. The total information content of the set A is then n times IC.

It is to be emphasized that information content of a graph G is not uniquely defined. It depends on the way the set A is derived from G as well as on the equivalence relation(s) which partition A into disjoint subsets A_i. So, for the same molecular graph (structure), different methods may give different numerical measures of information theoretic complexity.

6. Why and How Structure Is Related to Function?

Chemists often discuss the relationship between structure and property or reactivity using the IF-THEN type of structural rules. But it was not often recognized that the two-dimensional chemical structure so familiar to the chemists is a mathematical object which can be manipulated using mathematical formalisms. Mathematical chemistry derived from molecular graph theory and information theory made an enormous progress starting at the second half of the twentieth century. The relation between structure and function is guided by the ‘structure-property similarity principle’, which states that similar structures usually have similar functions or properties (Johnson et al. 1988). When one represents a molecule using a small number of structural attributes, intuitive IF-THEN rules can serve the purpose of relating structure to function. But when the attributes or descriptors are numbered in the hundreds or thousands, an intuitive approach of relating structure to function is not very effective. As noted by Bertrand Russell:

Intuition, in fact, is an aspect and development of instinct, and, like all instincts, is admirable in those customary surroundings which have moulded the habits of the animal in question, but totally incompetent as soon as the surroundings are changed in a way which demands some non-habitual mode of action. (Russell 1950)

Therefore, robust models derived from proven methods like multivariate statistics (Hawkins et al. 2000, 2003), partial order theory (Restrepo et al. 2011) need to be applied in understanding the structural basis of property, activity and reactivity of molecules using the plethora of mathematical descriptors that are available from contemporary mathematical chemistry and computer algorithms and software.

7. Conclusion

Currently, mathematical chemistry is an emerging field in which both basic research and applications are progressing simultaneously. Major developments in the modern trends of the field began in the second half of the twentieth century. This research was fueled mainly by two important factors: (a) the development of a plethora of new ideas for the representation and characterization of molecular structure using mathematics, and (b) applications of descriptors formulated by mathematical chemists to solve practical problems of combinatorial chemistry, new drug discovery, environmental protection, chemoinformatics, and bioinformatics. Whereas mathematical modeling, including mathematical chemistry, strives to find general principles to explain natural phenomena, a large part of chemistry involves studies of chemical problems in specific situations. As pointed out by K. Fukui:

Even the same atoms of the same element, when they exist in different molecules, exhibit different behaviors. The chemical symbol H even seems to signify atoms of a completely different nature. In chemistry, this terrible individuality should never be avoided by ‘averaging’, and, moreover, innumerable combinations of such atoms form the subject of chemical research, where it is not the ‘whole assembly of compounds of different kinds but each individual kind of compounds’ that is of chemical interest. On account of this formidable complexity, chemistry possesses inevitably one aspect of depending on the analogy through experience. This is in a sense said to be the fate allotted to chemistry, and the source of a great difference in character from physics. (Fukui (1982)

On the other hand, graph theory, which constitutes a major basis of mathematical chemistry, is a subject of a very general nature. As indicated by Frank Harary (1986), "It is because of this general nature that graph-theoretic methods have been used for characterizing structure in such diverse areas as theoretical physics, chemistry, biological and social sciences, engineering, computer science and linguistics." Applications of concepts derived from chemical graph theory and mathematical chemistry to a diversity of problems, e.g., characterization of structures of small molecules, quantification of DNA and protein sequences, numerical characterization of proteomics maps understanding the evolutionary changes in chemical biological interaction in the development of drug resistance, may be looked upon as an "isomorphism of phenomena in different fields of science" at the very fundamental level (Von Bertalanffy 1950). Balaban (2005) described how mathematics and chemistry have interacted fruitfully for the benefit of both. Rouvray, the founder of the Journal of Mathematical Chemistry, wrote the following in the Editorial Foreword of the journal:

Cross-fertilization of mathematical theory with chemical concepts has been responsible for the growth of major areas of chemistry over the past two centuries. The ongoing mathematization of chemistry shows no sign of abating and has in fact gained significantly in pace in recent years. This is a process we welcome and one that we view as a natural concomitant of the evolution of chemistry as a whole. We believe that the future vitality of chemistry is very much linked to the cultivation of new mathematical models and techniques which can be used to characterize chemical systems. (Rouvray 1987)

It is clear from the above that mathematical chemistry has made and will continue to make significant contributions to our understanding of chemistry via the application of mathematical concepts on chemical systems.

References

Artmann, B.: 1988, ‘The liberal arts’, Mathematical Intelligencer, 20, 40-1.

Atalay, B.: 2006, Math and the Mona Lisa: The art and science of Leonardo da Vinci, Washington, DC: Smithsonian, p. 26.

Balaban, A.T.: 1976, Chemical applications of graph theory, London: Academic Press.

Balaban, A.T.: 2005, ‘Reflections about mathematical chemistry’, Foundations of Chemistry, 7, 289-306.

Balasubramanian, K. & Basak, S.C.: 1998, ‘Characterization of isospectral graphs using graph invariants and derived orthogonal parameters’, Journal of Chemical Information and Computer Sciences, 38, 367-73.

Balasubramanian, K.: 2002, ‘Combinatorial enumeration of Ragas (scales of integer sequences) of Indian music’, Journal of Integer Sequences, 5, 1-21.

Basak, S.C.: 1987, ‘Use of molecular complexity indices in predictive pharmacology and toxicology: A QSAR approach’, Medical Science Research, 15, 605-9.

Basak, S.C.; Magnuson, V.R.; Niemi, G.J. & Regal, R.R.: 1988a, ‘Determining structural similarity of chemicals using graph-theoretic indices’, Discrete Applied Mathematics., 19, 17-44.

Basak, S.C.; Harriss, D.K. & Magnuson, V.R.: 1988b, POLLY v. 2.3, University of Minnesota.

Basak, S.C.; Niemi, G.J. & Veith, G.D.: 1991, ‘Predicting properties of molecules using graph invariants’, Journal of Mathematical Chemistry, 7, 243-72.

Basak, S.C.; Gute, B.D. & Grunwald, G.D.: 1997, ‘Use of topostructural, topochemical, and geometric parameters in the prediction of vapor pressure: A hierarchical approach’, Journal of Chemical Information and Computer Sciences, 37, 651-5.

Basak, S.C.; Grunwald, G.D.; Host, G.E.; Niemi, G.J. & Bradbury, S.P.: 1998, ‘A comparative study of molecular similarity, statistical and neural network methods for predicting toxic modes of action of chemicals’, Environmental Toxicology and Chemistry, 17, 1056-64.

Basak, S.C.; Balasubramanian, K.; Gute, B.D.; Gorczynska, A. & Roszak, S.: 2003a, ‘Prediction of cellular toxicity of halocarbons from computed chemodescriptors: A hierarchical QSAR approach’, Journal of Chemical Information and Computer Sciences, 43, 1103-9.

Basak, S.C.; Mills, D.; Mumtaz, M.M. & Balasubramanian, K.: 2003b, ‘Use of topological indices in predicting aryl hydrocarbon (Ah) receptor binding potency of dibenzofurans: A hierarchical QSAR approach’, Indian Journal of Chemistry, 42A, 1385-91.

Basak, S.C.; Gute, B.D.: 2008, ‘Mathematical biodescriptors of proteomics maps: Background and applications’, Current Opinion in Drug Discovery & Development, 11, 320-6.

Basak, S.C. & Mills, D.: 2009, ‘Mathematical chemistry and chemobioinformatics: A holistic view involving optimism, intractability, and pragmatism’, in: A. Graovac; I. Gutman & D. Vukičević (eds.), Mathematical methods and modeling for students of chemistry and biology, Zagreb: Hum Copies, pp. 211-42.

Basak, S.C.: 2010, ‘The role of mathematical chemodescriptors and proteomics based biodescriptors in drug discovery’, Drug Development Research, 72, 1-9.

Basak, S.C.; Mills, D.; Gute, B.D.; Balaban, A.T.; Basak, K. & Grunwald, G.D.: 2010, ‘Use of mathematical structural invariants in analyzing, combinatorial libraries: A case study with psoralen derivatives’, Current Computer-Aided Drug Design, 6, 240-51.

Basak, S.C.; Mills, D. & Hawkins, D.M.: 2011, ‘Characterization of dihydrofolate reductases from multiple strains of Plasmodium falciparum using mathematical descriptors of their inhibitors’, Chemistry and Biodiversity, 8, 440-53.

Bonchev, D. & Trinajstić, N.: 1977, ‘Information theory, distance matrix and molecular branching’, Journal of Chemical Physics, 67, 4517-33.

Bonchev, D.: 1983, Information theoretic indices for characterization of chemical structure, Chichester: Research Studies Press.

Bonchev, D.: 2009, ‘Information theoretic measures of complexity’, in: R. Meyers (ed.), Encyclopedia of complexity and system science, Heidelberg: Springer, Vol. 5, pp. 4820-38.

Bunge, M.: 1973, Method, model and matter, Boston: Reidel.

Caleon, I. & Ramanathan, S.: 2008, ‘From music to physics: The undervalued legacy of Pythagoras’, Science and Education, 17, 449-56.

Cayley, A.: 1857, ‘On the theory of the analytical forms called trees’, Philosophical Magazine, 13, 172-6.

Dampier, W.C.: 1961, A history of science and its relations with philosophy and religion, Cambridge: Cambridge University Press, p. 17.

Datta, B.: 2004, ‘Vedic mathematics’, in: P. Ray & S.N. Sen (eds.), The cultural heritage of India, Kolkata: The Ramakrishna Mission Institute of Culture, vol. VI, pp. 18-35.

Dehmer, M.: 2008, ‘Information-theoretic concepts for the analysis of complex networks’, Applied Artificial Intelligence, 22, 684-706.

Fukui, K.: 1982, ‘The role of frontier orbitals in chemical reactions (Nobel lecture)’, Angewandte Chemie International Edition, 21, 801-9.

Ghosh, A.; Nandy, A.; Nandy, P.; Gute, B.D. & Basak, S.C.: 2009, ‘Computational study of dispersion and extent of mutated and duplicated sequences of the H5N1 influenza neuraminidase over the period 1997−2008’, Journal of Chemical Information and Modeling, 49, 2627-38.

Ghosh, A. & Nandy, A.: 2011, ‘Graphical representation and mathematical characterization of protein sequences and applications to viral proteins’, Advances in Protein Chemistry and Structural Biology, 83, 1-42.

Hall, L.H.: 1996, Users guide, Molconn-Z, Software for computation of topological indices version for internet, Quincy, MA: Hall Associates Consulting.

Hall, L.H.: 2012, ‘Development of structure information from molecular topology for modeling chemical and biological properties: A tribute to the creativity of Lemont Burwell Kier on his 80^th birthday’, Current Computer-Aided Drug Design, 8, 93-106.

Harary, F.: 1969, Graph theory, Reading: Addison Wesley.

Harary, F.: 1986, ‘Graph theory as applied mathematics’, Journal of Graph Theory, 10, iii–iv.

Hardy, G.H.: 1921, ‘Srinivasa Ramanujan’, Proceedings of the London Mathematical Society, s2-19.

Hawkins, D.M.; Basak, S.C. & Shi, X.: 2000, ‘QSAR with few compounds and many features’, Journal of Chemical Information and Computer Sciences, 41, 663-70.

Hawkins, D.M.; Basak, S.C. & Mills, D.: 2003, ‘Assessing model fit by cross-validation’, Journal of Chemical Information and Computer Sciences, 43, 579-86.

Helmholtz, H.: 1964, On the sensations of tone, New York: Dover, pp. 234-49.

Hosoya, H.: 1971, ‘A newly proposed quantity characterizing topological nature of structural isomers of saturated hydrocarbons’, Bulletin of the Chemical Society of Japan, 44, 2332-9.

Janežič, D.; Miličević, A.; Nikolić, S. & Trinajstić, N.: 2007, Graph theoretic matrices in chemistry, Kragujevac: University of Kragujevac.

Johnson, M.; Basak, S.C. & Maggiora, G.: 1988, ‘A characterization of molecular similarity methods for property prediction’, Mathematical and Computer Modeling, 11, 630-4.

Kier, L.B. & Hall, L.H.: 1986, Molecular connectivity in structure-activity analysis, Letchworth: Research Studies Press.

Kier, L.B. & Hall, L.H.: 1999, Molecular structure description: The electrotopological state, San Diego: Academic Press.

Kline, M.: 1972, Mathematical thought from ancient to modern times, Oxford: Oxford University Press, vol. 1, p. 224.

Nandy, A.; Harle, M. & Basak, S.C.: 2006, ‘Mathematical descriptors of DNA sequences: Development and application’, Arkivoc, 9, 211-38.

Natarajan, R. & Basak, S.C.: 2011, ‘Numerical descriptors for the characterization of chiral compounds and their applications in modeling biological and toxicological activities’, Current Topics in Medicinal Chemistry, 11, 771-87.

Nath, S. & Bag, A.K.: 2004, ‘Post-Vedic mathematics’, in: P. Ray & S.N. Sen (eds.), The cultural heritage of India, Kolkata: The Ramakrishna Mission Institute of Culture, vol. VI, pp. 36-55.

Papadopoulos, A.: 2002, ‘Mathematics and music theory: From Pythagoras to Rameau’, Mathematical Intelligencer, 24, 65-73.

Popper, K.:1992, The logic of scientific discovery, London and New York: Routledge.

Primas, H.: 1983, Chemistry, quantum mechanics and reductionism, Berlin: Springer.

Randić, M.: 1975, ‘Characterization of molecular branching’, Journal of the American Chemical Society, 97, 6609-15.

Randić, M.: 1984, ‘On molecular identification number’, Journal of Chemical Information and Computer Sciences, 24, 164-75.

Randić, M.; Vračko, M.; Nandy, A. & Basak, S.C.: 2000, ‘On 3-D graphical representation of DNA primary sequences and their numerical characterization’, Journal of Chemical Information and Computer Sciences, 40, 1235-44.

Randić, M. & Basak, S.C.: 2001, ‘On use of the variable connectivity index ^1f in QSAR: Toxicity of aliphatic ethers’, Journal of Chemical Information and Computer Sciences, 41, 614-8.

Randić, M; Witzmann, F.; Vračko, M; Basak, S.C.: 2001, ‘On characterization of proteomics maps and chemically induced changes in proteomes using matrix invariants: Application to peroxisome proliferators’, Medicinal Chemistry Research, 10, 456-79.

Randić, M.; Zupan, J.; Balaban, A.T.; Vikić-Topić, D. & Plavšić, D.: 2011, ‘Graphical representation of proteins’, Chemical Reviews, 111, 790-862.

Rashevsky, N.: 1955, ‘Life, information theory, and topology’, The Bulletin of Mathematical Biophysics, 17, 229-35.

Ray, P.: 2004, ‘Chemistry in ancient and medieval India’, in: P. Ray & S.N. Sen (eds.), The cultural heritage of India, Kolkata: The Ramakrishna Mission Institute of Culture, vol. VI, pp. 136-51.

Raychaudhury, C.; Ray, S.K.; Ghosh, J.J.; Roy, A.B. & Basak, S.C.: 1984, ‘Discrimination of isomeric structures using information theoretic topological indices’, Journal of Computational Chemistry, 5, 581-8.

Restrepo, G.; Brüggemann, R. & Klein, D.J.: 2011, ‘Partially ordered sets: Ranking and prediction of substances’ properties’, Current Computer-Aided Drug Design, 7, 133-45.

Restrepo, G. & Villaveces, J.L.: 2012, ‘Mathematical thinking in chemistry’, Hyle – International Journal for Philosophy of Chemistry, 18, 3-22.

Rouvray, D.H.: 1987, ‘Editorial Foreword’, Journal of Mathematical Chemistry, 1, i-iv.

Russell, B.: 1950, Mysticism and logic, London: George Allen & Unwin.

Semichem: 2012, CODESSA: Quantitative Structure/Property Relationships [online at: http://www.semichem.com/codessa/codrefs.php, accessed February 2012].

Shannon, C.E.: 1948, ‘A Mathematical Theory of Communication’, The Bell System Technical Journal, 27, 379-423.

Schrödinger, E.: 1954, Nature and the Greeks, Cambridge: Cambridge University Press, p. 30.

Schummer, J.: 1998, ‘The chemical core of chemistry I: A conceptual approach’, Hyle – International Journal for Philosophy of Chemistry, 4, 129-62.

Sylvester, J.J.: 1878, ‘On an application of the new atomic theory to the graphical representation of the invariants and covariants of binary quantics, with three appendices’, American Journal of Mathematics, 1, 64-125.

Tarakeswara, R.B. & Prasad R.P.V.G.D.: 2011, ‘A novel process for Melakartha Raaga recognition using hidden Markov models (HMM)’, International Journal of Research and Reviews in Computer Science, 2, 508-13.

Todeschini, R.: 2004, DRAGON 5 version - software for molecular descriptors, [online at: http://www.ccl.net/qsar/archives/0403/0458.html, accessed February 2012].

Trinajstić, N.: 1997, ‘Mathematics and chemistry: The unlikely partners’, in: D.H. Rouvray (ed.), Concepts in chemistry: A contemporary challenge, Taunton: Research Studies Press, pp. 17-39.

Von Bertalanffy, L.: 1950, ‘An outline of general system theory’, British Journal for the Philosophy of Science, 1, 134-165.

Weininger, S.J.: 1984, ‘The molecular structure conundrum: Can classical chemistry be reduced to quantum chemistry?’, Journal of Chemical Education, 61, 939-43.

Wiener, H.: 1947, ‘Structural determination of paraffin boiling points’, Journal of the American Chemical Society, 69, 17-20.

Subhash C. Basak:
International Society of Mathematical Chemistry, 1802 Stanford Avenue, Duluth, MN 55811, USA; & Natural Resources Research Institute and Department of Chemistry, University of Minnesota Duluth, 5013 Miller Trunk Highway, Duluth, MN 55811, USA; sbasak@d.umn.edu