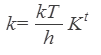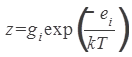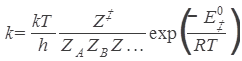http://www.hyle.org
Copyright © 2012 by HYLE and Hinne Hettema
The Unity of Chemistry and Physics:
|
||||||||||||||||||||||||||
|
Table 1: Wigner’s three threes that characterize transition state theory (after Miller 1998). |
|
| Three steps in the theory of kinetics | |
|
WS1 |
Determine potential energy surfaces |
|
WS2 |
Determine elementary reaction rates |
|
WS3 |
Solve rate equations for complex reaction mechanism |
| Three groups of elementary reactions | |
|
WG1 |
Vibrationally/rotationally inelastic collisions (not a chemical reaction) |
|
WG2 |
Reactive collisions on a single potential energy surface |
|
WG3 |
Electronically non-adiabatic reactive collisions |
| Three assumptions | |
|
WA1 |
Electronic adiabaticity: the electronic configuration is in the lowest quantum state for each configuration of the nuclei |
|
WA2 |
The validity of classical mechanics for the nuclear motion |
|
WA3 |
Existence of a dividing surface that trajectories do not re-cross |
Wigner referred to the theory in this paper as ‘The Transition State Method’ and distinguished three steps. WS1: The determination of potential energy surfaces, which gives "the behaviour of all molecules present in the system during the reaction, how they will move, and which products they will yield when colliding with definite velocities, etc." (Wigner 1938, p. 29). The solution of this problem requires the calculation of a potential energy surface, which is a quantum chemistry problem. WS2: The next step is the calculation of ‘elementary reaction rates’. WS3: The third problem is to combine these ‘elementary’ reactions into a series of reactions which make up the overall chemical transformation. Of these, the ‘elementary’ form of reaction rate theory only considers WS1 and WS2 and ignores WS3.
Wigner classified the elementary reactions in three groups: inelastic collisions, in which the molecules exchange vibrational and/or rotational energy but do not change their chemical composition, reactions on a single potential energy surface which involve no change in electronic quantum numbers, and reactions involving multiple potential energy surfaces (non-adiabatic reactions). Only the second type of elementary reactions can be treated with transition state theory, hence, only WG2 is considered in the theory. Finally, Wigner discussed three assumptions. The first one is the adiabatic assumption (WA1), which assumes that during the reaction the molecular system ‘stays’ on the lowest possible potential energy surface and there is no change of electronic configuration. The second assumption is that the motion of the nuclei can be described with classical mechanics (WA2). The third assumption requires that the reaction does not go ‘backwards’, i.e. all systems crossing the barrier are reacting systems (WA3). The consequence of this is that the step from the reactants to the transition state is the rate determining step for the equation. Once a set of reactants form a transition state, this transition state will fall apart to form the end products of the reaction. Therefore, WA3 adds additional precision to the specification of the transition state.
The three threes form a more elaborate formulation of the Eyring conditions (E1-E3) in the sense that they add precision and in this way also indicate directions for future research (e.g. reactions on non-adiabatic surfaces, quantum effects in nuclear motion, etc.).
2.3 Summary
The structure of absolute reaction rate theory is given in Figure 3. The purpose of the theory was to provide exact expressions for the two values E and A. From the viewpoint of quantitative explanations for these quantities the theory has been moderately successful, but has, in the words of Laidler and King (1983), "its difficulties".
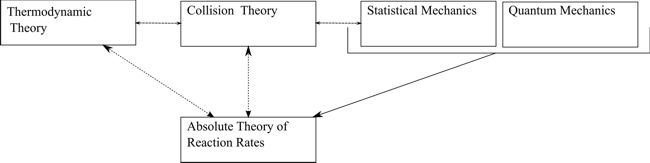
Figure 3: The conceptual structure of the absolute reaction rate theory and its comparisons to the thermodynamic theory and collision theory. The arrows indicate structural relationships between the theories.
Historically the theory was not immediately accepted upon its appearance. As is seen in the proceedings of the 67th general discussion of the Faraday Society (which was held at the University of Manchester, 13-15 September 1937), there were some who saw the theory as somewhat speculative.
However, the most interesting aspect of the absolute reaction rate theory is that it provided a
[…] conceptual framework with the aid of which experimental chemists (and others) can gain some insight into how chemical processes occur. On this score the theory must receive the highest marks; for nearly half a century it has been a valuable working tool for those who are not concerned with the calculation of absolute rates but are helped by gaining some insight into chemical and physical processes. The theory provides both a statistical-mechanical and a thermodynamic insight – one can take one’s choice or use both formulations. [Laidler & King 1983, p. 2664]
Thus, in the final analysis, the achievement of the theory was primarily conceptual: it provided valuable insights into the mechanisms that drive chemical reactions at a molecular level. Hence, the absolute theory of reaction rates is a very strong example for the unity of science – it is precisely one of those examples where it is hard to imagine chemistry without physics, but at the same time it is a ‘chemical’ theory in that it focuses on molecules, molecular structures, and transformations.
The remainder of this paper will be concerned with how the absolute theory of reaction rates fits philosophical conceptions of the unity of science. From the viewpoint of reduction and unity of science, the theory has a number of unique features:
- The introduction and specification of the transition state in terms of a specific location on the potential energy surface of the reaction and its characterization as a molecule with specific properties;
- The degree to which explanation depends on comparison between the collision, thermodynamic, and quantum mechanical/statistical mechanical formulations of molecular quantities.
If it is the case that the unity of science is the end product of some process of theory reduction, then this case should fit a reductive model. Similarly, if the unity of science is not based on a reductive model, there should be a fit with one of the non-reductive proposals.
In the next section it is my aim to discuss some approaches to the topic of reduction before returning to the question how the theory of absolute reaction rates might fit a reductive model and what the consequences of such a fit might be.
3. The unity of science: reductive, non-reductive, and naturalized approaches
In this section, it is my aim to present the Nagelian approach to reduction as a ‘close reading’ of the form in which it was originally given by Nagel (1961), as well as to outline some aspects of the recent interpretation of Nagel’s theory. I then discuss a number of non-reductive approaches, and conclude with a proposal for a ‘naturalized’ Nagelian reduction model that combines important aspects of a defensible Nagelian model with non-reductive approaches, and which is adaptable to interesting cases of scientific explanation. The key concept of ‘naturalized’ Nagelian reduction is that the philosophical notion of reduction should be a paraphrase, in some formal language, of what happens when scientists claim that one theory explains another. The concept is discussed in more detail in Section 3.3.
3.1 Nagelian Reduction
Nagel’s formal requirements for reduction are well known and are generally taken to be the requirements of connectibility and derivability, stating that a linguistic connection between the languages of the reduced and reducing theory has to exist, and that the reduced theory has to be derivable from the reducing theory cum ‘reduction postulates’. Of the formal conditions, especially the notion of connectibility requires further consideration.
To begin with, the reduced and reducing sciences usually have a number of terms in common (Nagel 1961, p. 351-2). While the meaning of these terms is fixed by procedures internal to both sciences, the meanings of terms of a certain ‘common vocabulary’ will coincide sufficiently to pose no further problems for derivability. On the other hand, there is also a class of terms which occur in the reduced science but not in the reducing one. Hence, derivability can only be achieved when the concepts native to the reduced science can be explicated in terms of the reducing one.
To achieve connectibility, Nagel introduced, in addition to the formal requirements, the notion of coordinating definitions (here called ‘reduction postulates’) as an additional assumption. The reduction postulates ‘modifies’ the reducing science to overcome the issue that, as Nagel states, derivation is impossible if the premise of the argument (i.e. the reducing science) does not already contain the necessary concepts of the reduced science. Hence, the reducing science has to state, in some meaningful sense, what the concepts of the reduced science are. The reduction postulates stipulate
suitable relations between whatever is signified by ‘A’ and traits represented by the theoretical terms already present in the primary science [ibid., pp. 353-4].
While the role of the reduction postulates is simple enough, the exact formulation of the reduction postulates themselves is far from simple. For instance, Nagel discussed three possible kinds of linkages postulated by reduction postulates (ibid.), which can be paraphrased as follows:
- The links are logical connections, such that the meaning of ‘A’ as ‘fixed by the rules or habits of usage’ is explicable in terms of the established meanings of the theoretical primitives in the primary discipline.
- The links are conventions or coordinating definitions, created by ‘deliberate fiat’, which assigns a meaning to the term ‘A’ in terms of the primary science, subject to a criterion of consistency with other assignments.
- The links are factual or material, or physical hypotheses, and assert that existence of a state ‘B’ in the primary science is a sufficient (or necessary and sufficient) condition for the state of affairs designated by ‘A’. In this scenario, the meanings of ‘A’ and ‘B’ are not related analytically.
It is thus important to realize that Nagel’s criteria for reduction postulates are open to a number of interpretations, and can be instantiated in actual practice in a number of ways. Specifically, as also Klein (2009) has argued, the reduction postulates refer to the representational power of the reducing theory; its ability to introduce the terms present in the reduced science. Note that Nagel’s second formal requirement states that the terms are fixed by meanings and use local to the relevant theory and hence this sort of representational power is not a trivial requirement.
The Nagelian derivability condition states:
[…] a reduction is effected when the experimental laws of the secondary science (and if it has an adequate theory, its theory as well) are shown to be the logical consequences of the theoretical assumptions (inclusive of the coordinating definitions) of the primary science. [Nagel 1961, p. 352]
In addition to the formal requirements, Nagel specified a number of informal requirements. These introduce many qualifications and conditions that will prove to be relevant in what follows. Moreover, the informal requirements contain many qualifications to the reduction scheme that are commonly overlooked.
The main reason for introducing the informal requirements is that the formal requirements are, by themselves, incapable of distinguishing between worthwhile and worthless theory reductions. As Nagel noted, the formal conditions could in many cases be satisfied rather trivially with some ad hoc assumptions. The informal conditions are there to block this sort of trivial reduction.
The first informal requirement is that of (external) corroboration of the reducing theory. That helps in the unification of the sciences by expanding their domains of applicability, and strengthens the case for the corroboration of the reducing theory.
The second informal requirement is that of maturity of the reducing theory. As Nagel notes, the ideal gas law could be reduced to the kinetic theory of gases only after the formulation of Boltzmann’s statistical interpretation of the second law of thermodynamics, and similarly the reduction needs a sufficiently mature mechanics to be counted as a success.
Perhaps the most important requirement for the further discussion of the reduction of chemistry to physics, and one often overlooked in this context, is the third one. Nagel claimed that it is frequently a mistake to assume that reduction amounts to the derivation of the properties of one subject matter from the properties of another, and therefore denies that the reduced science can be eliminated on the basis of such property reduction, and that, in fact, "the conception of reduction as the deduction of properties from other properties is potentially misleading and generates spurious problems" (ibid., p. 364). Instead, Nagel argued that the various ‘properties’ ascribed to chemical elements, for instance, are the end result of theories about chemical elements. If such theories are later shown to be reducible to theories of atomic physics, then this proves the existence of a logical relationship between theories, but does not provide an argument for the reduction of the essential ‘natures’ of the concepts that function in these theories.
It is thus important to note that Nagel did not defend a form of reductionism that allows for a ‘nothing but’ approach to reduction. Specifically, he did not defend a view where for instance an atom can be said to be ‘nothing but’ a collection of a nucleus with a certain number of electrons. While it is formally required to make such a statement in order for the reducing theory to be able to say something about atoms in the first place, the requirement is a formal and not an ontological one.
This is an important point precisely because this third informal requirement establishes the ontological independence of the reduced science: in many cases of reduction, the existence of reduction is a matter of the existence of a logical or formal relationship between the reduced theory and the reducing theory cum the reduction postulates, where the latter allow a formal derivation relationship but do no ontologically heavy lifting.
Philosophers of science have tended to focus on the formal requirements over the informal requirements, and argued that the connectibility requirements (or ‘reduction postulates’) specify ontological identities. The notion that reduction postulates have to represent identities was most strongly defended by Causey (1977). He analyzed sentences of the form:
∀ x: α x ↔ β x
and noted that, when we have a true sentence of this form, it could be either one of three cases (i) α and β are accidentally co-extensional, (ii) α and β are nomologically correlated (and co-extensional), or (iii) α and β are are identical. On Causey’s analysis, (i) can be ignored, while (ii) is question begging as a reduction sentence and only (iii) leads to an acceptable reduction sentence. As he noted with regard to (ii), the concept of an ACCS (Attribute Correlation Connection Sentence):
By now it should be fairly clear that […] mere attribute-correlation law sentences, are not acceptable as connecting sentences. ACCS’s are mysterious, causal law-sentences that are themselves in need of explanation. If they are used as connecting sentences […] then we do not explain T2 in terms of the laws of T1 but rather in terms of T1 plus these mysterious correlation laws. [Ibid., p. 86]
Hence Causey concluded that adequate correlations of the form (7) require "thing-identities" and "attribute identities" (ibid., p. 79).
Recently, the pendulum on Nagelian reduction has swung the other way. Klein (2009) and van Riel (2011) have argued that Nagelian reduction should not be read as a defense of ontological reductionism. Klein argues that Nagel’s condition of connectibility focuses on the degree to which the reducing theory can represent notions of the reducing theory. Similarly, van Riel argues that the way in which Nagel’s framework for reduction is commonly read does not correctly represent the ‘careful remarks’ about the inter-theoretic relationships that accompanied it.
Dizadji-Bahmani, Frigg & Hartmann (2010) argue that a ‘generalized Nagel-Schaffner model’, in which the reduction postulates are factual claims, is alive and well. An overview of their proposal is presented in Figure 4.
They defend the generalized Nagel-Schaffner model against seven specific objections, concluding that none of them apply. In their terminology, the generalized Nagel-Schaffner model consists of a theory TP reducing to a theory TF through the following steps:
- The theory TF is applied to a system and supplied with a number of auxiliary assumptions, which are typically idealizations and boundary conditions.
- Subsequently, the terms in the specialized theory T*F are replaced with their ‘correspondents’ via bridge laws, generating a theory T*P.
- A successful reduction requires that the laws of T*P are approximately the same as the laws of the reduced theory TP and hence between T*P and TP there exists an analogy relation.

Figure 4: Overview of the generalized Nagel-Schaffner reduction proposed by Dizaje et al. 2010.
Specifically, two features of the generalized Nagel-Schaffner model are worth noting. The first one is that in this model the reduction postulates are part of the reducing theory, rather than some auxiliary statements that have a primarily metaphysical import. Specifically, Dizadji-Bahmani et al. argue that of the three types of linkages that may be expressed by reduction postulates, the first two can be discarded and reduction postulates express matters of fact. This is so, because the aim of scientific explanation is neither "metaphysical parsimony" nor "the defense of physicalism" (ibid., p. 405). They argue for a naturalized reading of Nagel, in which the aim of reduction is consistency between the reduced and reducing theory, and confirmation of TP entails confirmation of TF for domains where there is significant overlap.
In this manner, Dizadji-Bahmani et al. claim that reductions have a high likelihood of occurring in situations, such as the present case of the unity between chemistry and physics, where theories have an overlapping target domain:
We are committed to the claim that if we have a situation of the kind described above (in which the two theories have an overlapping target domain), then one must have a reduction. [Ibid., p. 410]
3.2 Non-reductive approaches to the unity of science
In this section, I will discuss some of the non-reductive approaches that may assist in understanding and characterizing the relationship between theories of physics and theories of chemistry. The examples are Darden and Maull’s notion of an ‘interfield’ theory, and various approaches to accommodation and structural similarity. I will not focus on non-reductive theories, such as the approach by Dupré (1993), which advocate disunity.
The first model we will consider is that of ‘interdisciplinarity’. The promise of the ‘interdisciplinarity’ or ‘interfield theory’ approach is that it can provide a non-reductive model for the unity of science, in which both chemistry and physics play an equal part in the relationship.
One of the theories proposed to this end is the concept of an ‘inter-field theory’ proposed by Darden & Maull (1977). The notion of a ‘field’ is basic to the model. A field is characterized (along the lines developed in Shapere 1977) as based on an ‘ordered domain’ of phenomena, to which it introduces a specific set of practices and techniques, perhaps with some local theories:
Local theories that are specific to a field are called ‘intrafield’ theories. Fields and intrafield theories cannot be equated. Several, sometimes competing, theories are possible: A field at one point in time may not contain a theory, or may consist of several competing theories, or may have one rather successful theory. [Darden & Maull 1977, p. 48]
In this manner, fields are not competing in the same way as theories, and it is also not possible to say that one ‘field’ may ‘reduce’ another: the necessary (Nagelian) relationships for theory reduction cannot obtain between fields. Interfield theories are specific theories which use concepts and data from neighboring fields. The definition of an interfield theory is a theory that does some or all of the following (ibid., p. 59):
- To solve (perhaps ‘correctly’) the theoretical problem which led to its generation, that is, to introduce a new idea as to the nature of the relations between fields;
- To answer questions which, although they arise within a field, cannot be answered using the concepts and techniques of that field alone;
- To focus attention on previously neglected items of the domains of one or both fields;
- To predict new items for the domains of one or both fields;
- To generate new lines of research which may, in turn, lead to another interfield theory.
Yet it is hard to see that the ‘interfield’ concept would be incompatible with a local version of the naturalized Nagelian reduction we developed in the previous section. Fields can be populated by theories, and reduction relationships in a Nagelian sense may exist between theories in different fields. In this regard it is especially worth noting that the reading of the reduction postulates as ‘matters of fact’ plays the role of establishing the interfield theory to a significant degree.
?In a recent paper, Harris (2008) has argued that the early theories of the chemical bond are best conceived as an interdisciplinary entity, which draws equally on physics and chemistry. According to Harris, the hallmark of this interdisciplinary entity is the cooperation between chemists and physicists on problems of common interest:
[…] physics and chemistry were discovering problems of collaborative value within a common theoretical framework. There is no avoiding the fact that until physical methods were available to chemists, there was no real possibility of discovering the mechanism of bonding. [Harris 2008, p. 88]
Harris argues that from this perspective, the claim that chemistry was reduced to physics has to be revised, since the assumption that a successful reduction was the prime consequence of this interdisciplinarity does not properly assess the historical facts and the value of the interdisciplinarity to both physicists and chemists. Harris’ argument is primarily historic. She contrasts the interdisciplinary relationship with a reductive relationship which she does not flesh out in a lot of detail but describes in terms of an attempted takeover, quoting Born where he expressed "a belief that the ‘vast territory of chemistry’ was not only important for physicists to explore, but that this work was necessary in order for physicists to ‘impose her laws upon her sister science" (Born as quoted in ibid., p. 81).
Recently, there has also been renewed interest in the Neurathian program for the unity of science. The program was discussed by Cartwright et al. (1996) and Potochnik (2011) in the context of the unity of science. Neurath’s work is easily accessible in Cohen & Neurath 1983. He viewed the unity of science as part of a broader ‘encyclopedic’ program that was also educational in character. A characteristic of Neurath’s concept of the unity of science is that it has room for multiple explanations for a single phenomenon. Neurathian unity of science is closely linked to Duhemian holism, in the sense that hypotheses are tested in a holistic manner, against a unified whole of theoretical statements.
In this context, it is interesting to note that Spector (1978) has advanced claims very similar to those of Harris to argue precisely that the relationship is one of reduction, in fact, an entire branch reduction of chemistry to physics which seems to draw into question the notion of non-reducibility, as well as that of a further specification of the reduction relation in question.
In practice, the encyclopedic approach builds on what the initial sciences have to offer, and then starts looking at the sort of relationships that might hold between them. In his 1937 essay ‘The Departmentalization of Unified Science’, Neurath described the following approach to unification:
If one starts with a great many special disciplines […] overlapping one another, one might axiomatize all groups of statements ready for it. One might select all cases in which the logical structure of a group of statements is identical with the logical structure of another group. [Neurath 1983a, p. 202]
Neurath called this approach to the unity of science ‘encyclopedism’ and contrasted it to ‘pyramidism’. He viewed the latter as inspired by metaphysical views on the unity of science, in which:
Not a few classifications and arrangements of the sciences can be regarded as derivates from the architectonic structure of such metaphysics, even if their creators were interested in empiricism. [Ibid., p. 203]
Such a metaphysical commitment is a bad idea according to Neurath. Hence, the unity of science is not based on a hierarchical structure of nature, but rather on an encyclopedic model, in which one is
[…] satisfied with a rough bibliographic order for an initial orientations, made by librarians. [One] accepts the fact that the vast mass of the groups of statements are, as it were, in one place. Certain coherent forms could be arrived at by means of axiomatization or other procedures and a complicated network gradually created; there is no symmetrically pyramidical edifice. [Ibid., p. 204]
Neurath’s model is thus best characterized as anti-reductionist: the holistic criterion for acceptance of statements is whether they fit with an existing whole, and once constructed, many wholes might structurally connect with each other. In this way, Neurath allowed several competing explanatory systems to co-exist, and argued that some systems are better suited to provide explanations in given situations.
Alisa Bokulich (2008), in a study of the relationship between classical and quantum mechanics, develops a notion of (non-reductive) ‘interstructuralism’:
Interstructuralism is an approach to inter-theory relations that emphasizes the importance of structural continuities and correspondences in giving an adequate account of the relation between two theories. It recognizes a richer diversity of correspondence relations than does any form of reductionism or pluralism. [Bokulich 2008, p. 173]
Bokulich’ claim concerns specifically dynamical structures. From this perspective, she argues that there may be some question as to how this model would apply to different theory pairs, though she does mention chemistry as a potential candidate for such a relationship (ibid., p. 173). She presents interstructuralism as a middle path between reductionism and theoretical pluralism, which takes important lessons from either approach.
Especially, she argues that interstructuralism leaves the higher level theories (the ‘reduced’ theories in a reduction relationship) intact as explanatory theoretical entities in their own right. However, from reductionism she takes the idea that the domains of phenomena are not entirely distinct, and that in this sense, an overall theory of how these phenomena are related is bound to lead to new insights.
To the degree that Bokulich identifies ‘reductionism’ with the strict interpretation of Nagelian reduction as ‘identities’ cum ‘strict derivation’ (and her book suggests that she does) the approach I am advocating to Nagelian reduction is to a significant degree compatible with interstructuralism.
3.3 Naturalized reduction
In this paper, my proposal is to develop and defend a naturalized Nagelian reduction, which takes the Nagelian model as a heuristic model to inter-theory relationships in actual science. Candidate theories for the naturalized Nagelian reduction are those theories which claim explanations of (aspects) of one theory by another.
Naturalized Nagelian approach then proceeds along the following lines:
- First we seek out cases of claimed explanations in actual science.
- We then proceed to rationally reconstruct these cases of explanations.
- Subsequently, we seek to formulate a paraphrase of this rational reconstruction in terms of a (more or less formal) specification of both the basic assumptions and unique features of the explanation.
- Subsequently, we establish the necessary linkages which make the explanation work.
- Lastly, we evaluate the formal structure in terms of either a reductive or suitable non-reductive model of the unity of science.
The main reason for advocating a ‘naturalized’ conception of the Nagelian reduction as the correct relation of unity between chemistry and physics is that this seems to be one of the few conceptions of this relationship that is capable of dealing with the conceptual strength of chemical language.
It is by now well established in the philosophy of chemistry that the relationships between theories of chemistry and theories of physics do not fit the requirements of the Nagelian reduction model when it is read in terms of identities cum strict derivation. As the naturalized Nagelian reduction contends, it is explicitly non-eliminative; rather, Nagelian reduction aims to be a (logical) paraphrase of what exactly happens when one theory explains another.
The perceived disunity of the language of chemistry and physics is to a large degree responsible for the somewhat unfortunate introduction of the concept of ‘ontological reduction’ in the philosophy of chemistry, a blank cheque written to metaphysics in payment for the perceived failure of Nagelian reduction. It is the aim of naturalized Nagelian reduction to bounce that cheque, and reclaim room for theoretical explanation with ontological independence.
As stated in the introduction, my treatment of these issues in the present paper is mostly informal in order to bring out the approach. I have proposed a formal framework for naturalized reduction which is based on the structuralist approach to scientific theories in Hettema (2012).
4. Absolute reaction rates as a case study for naturalized reduction
In this section I consider absolute reaction rate theory as a case study for naturalized Nagelian reduction. The rational reconstruction required for our discussion is largely found in Section 2. The main aim of this section will be to discuss the structure of the theoretical framework and the linkages between the relevant components of the network. The sort of unity of science that is supported by the consideration of the absolute reaction rate theory is discussed in the next section.
The characterization of the linkages will involve a number of steps. The first step is the specification of the Nagelian connections between the theories that constitute the network of explanation. From these, I will draw two main conclusions which allow us to characterize the uniqueness of absolute reaction rate theory as a proposed case of reduction: in the first place, I argue that some elements of this theory remain unconnected, and hence are unique features of the theory, and secondly, the Nagelian connections, when read as statements of fact, allow us to specify the unique role played by comparison in the theory. The last step is the evaluation of the theory as a case study in naturalized Nagelian reduction. This will assist in further specifying some of the necessary detail of naturalized Nagelian reduction.
As I will argue in this section, the theory of absolute reaction rates exhibits a number of interesting features which prove to be unique features of the theory. These are a specification of the transition state and the degree to which the comparison of the three different approaches – statistical mechanics, collision theory, and thermodynamics – provides further insight into the calculation of the quantities A and EA. The combination of these two unique features gives rise to a third: the fact that in the absolute reaction rate theory multiple theories cooperate in the explanation. The role played by these unique features of the theory is specified in detail by the specification of the Nagelian connections.
4.1 Reduction between theories: Nagelian connections and derivations
The first step in the naturalized reduction program is to formally paraphrase the reduction of the Arrhenius equation by the various theories that constitute the net of absolute reaction rate theory. As we have seen in the previous discussion, the theory needs to explain the pre-exponential (or ‘frequency’) factor A and the activation energy EA. The formal paraphrase of ‘explanation’ in terms of reduction is Nagel’s formal conditions of connectibility and derivability. As was already indicated in the preceding sections, the contention of naturalized Nagelian reduction is that, of these conditions, ‘connectibility’ does a significant amount of scientific work, while derivability is a relatively pedestrian affair.
4.1.1 Activation energy
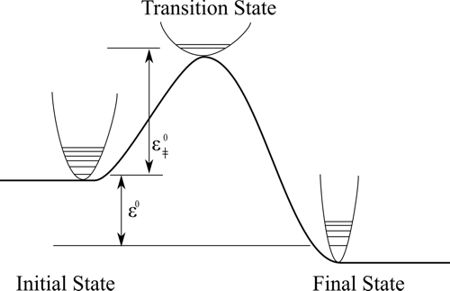
The activation energy may be identified with the difference in energy between the ground state of the reactants and the point on the potential energy surface which corresponds to the transition state – a molecular structure which can be specified with sufficient precision to allow its exact calculation (though within the limits of quantum chemical methods and approximations such as the Born-Oppenheimer approximation). Hence we have, I believe, a relatively non-contentious case for identification of the activation energy, under the condition that we define a transition state in terms of its location on the potential energy surface. The real work of the reduction is, however, done precisely by this condition.
The Nagelian ‘identification’ is thus a two-step process, which takes us from (i) a stipulation of a transition state in terms of a structure located at a particular location on the potential energy surface, to (ii) an identification of the activation energy in terms of the energy difference between the ground state and the transition state.
Eyring’s theory is noteworthy for the amount of precision it allows in the specification of the transition state at a molecular level. As we have seen, a background postulate which has no counterpart in the Arrhenius equation is that the reaction may be viewed as a translational motion along the reaction coordinate. Whereas the transition state was foreshadowed in the work of Arrhenius in the postulate of the ‘active’ form of cane sugar, the absolute theory of reaction rates is capable of explicating exactly what the transition state is. In brief, its structural features are:
- The motion along the reaction coordinate can be treated as a free translational motion.
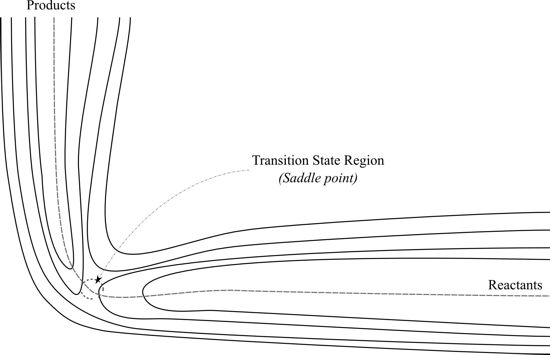
- The transition state lies at the ‘saddle point’ of the potential energy surface of the reaction.
- It is a ‘normal’ molecule in all other relevant respects.
It is worthwhile to investigate how this specification of the transition state relates to the basic assumptions of both Arrhenius’ equation and absolute reaction rate theory. It is particularly interesting in this context that the notion of the ‘transition state’ gains additional precision and is in particular by Eyring’s theory in terms of an
[…] ordinary molecule, processing all the usual thermodynamic properties, with the exception that motion in one direction, i.e. along the reaction coordinate, leads to decomposition at a definite rate. [Glasstone et al. 1941, p. 10-11]
In terms of a Nagelian model, it is thus not a case of straightforward identities cum derivation that leads to the specification of the activated state. Rather, the reduction postulate for the activation energy takes the form of a statement of fact, one that has taken hard work in the reducing theory to accomplish.
The fact that the reducing theory is transformed during the reduction is generally recognized in discussions of Nagelian reductions, as we have seen in our discussion of the model of Dizadji-Bahmani et al. (2010). In the present case it may be argued, however, that the specification of the transitions states does more than mere a transformation of the reducing theory: it interprets a specific feature of the reduced theory in terms of the reducing theory as a concept that does not flow ‘naturally’ from the reducing theory, and can only be properly understood from the viewpoint of the reducing theory itself.
Furthermore, this specification relies on several further theoretical concepts: the idea of a reaction as a translational motion along the reaction coordinate, as well as a structural characterization of the active complex as a particular type of molecule.
4.1.2 The Pre-exponential factor
In the statistical formulation of the theory, the frequency factor A is identified (apart from the factor kT/h) with a quotient of the partition functions of the activated state and the reactants. But this identification is not the compelling point of absolute reaction rate theory.
As in the case of the activation energy, the real work is done by the science itself. The compelling point is that this ‘identification’ allows for a mechanistic insight into the dynamics of a chemical reaction. The mechanism for this mechanistic insight is the comparison of several contending explanatory theories for the pre-exponential factor, which provide mechanisms in terms of intermolecular collisions or thermodynamic quantities.
The mechanistic features are quite easy to see for the simple collision theory. But since the collision theory needs to introduce a ‘fudge factor’ in the form of a ‘reactive probability’ P its predictive power is somewhat limited. The statistical mechanical theory fares better in this regard. With some simplifying assumptions, it is possible to construct explicit partition functions in terms of translational, rotational, and vibrational motion for the reactants and products, and hence gain significant insight into various types of reactions. Indeed, a large part of the book by Glasstone, Laidler & Eyring (1941) does precisely that.
The thermodynamic formulation of the reaction rate is another interesting feature of the theory. Thermodynamic quantities are in general macroscopic quantities, and Eyring’s thermodynamic formulation alongside the statistical mechanical formulation of the theory allows for a specification of thermodynamic energies and entropies of activation in terms of a mechanical model at the micro level.
The interpretation of the partition function can be seen, along the lines of Spector’s (1978) division of labor between the theoretical chemist and the theoretical physicist, as falling within the realm of "accounting for the arrangement and behavior of atoms and molecules […] on the basis of current physical theories regarding the structure of the atom and the laws concerning the behavior of its constituents" (even though Spector’s final conclusion, that this is eventually done with quantum mechanics, is incorrect in this context).
The fact that we can express A in terms of statistical mechanics or reinterpret it in terms of the collision theory forms an interesting (and complicating) feature of the classification of the present case as one of Nagelian reduction. These re-interpretations form an important component of the attractiveness of the theory, since they allow chemists to ‘shift perspective’ on the theoretical model where required, and cannot be ignored as a feature of reduction. It is in this context noteworthy that explanatory theories of weaker strength, such as for instance the collision theory, are not discarded in the explanation. Hence, the theory of absolute reaction rates forms a key example of cooperation between several reducing theories, which turns the reduction relation from one between two theories into an explanatory and comparative relation on a network of theories.
The comparison of different approaches in the calculation of the pre-exponential factor therefore has significant consequences for the philosophy of science: it establishes network of reducing theories that can be evaluated on a criterion of explanatory strength. The refinement and evaluation of the explanatory strength forms an important addition to the concept of Nagelian reduction, and moreover, is one that allows for disciplinary autonomy.
4.1.3 A theory net with local reductions
The explanation of reaction rates thus proceeds in the context of a net of theories, which is depicted in Figure 3. While connective and derivative links of a Nagelian sort exist between all these theoretical approaches, the reduction cannot be summarized as a relationship between two theories: the strength of the theory results from the detailed specification of the transition state which makes the identification possible, and the comparison it allows between the different approaches.
Hence in the case of absolute reaction rate theory the explanation proceeds in terms of multiple underlying theories, which in turn can be evaluated and compared on the amount of reductive strength that they are capable of providing.
In this sense, the intertheory relationships between chemistry and physics require a network of theories for their specification. This has a number of important consequences. In particular, it lends support to the characterization of absolute reaction rate theory as an interfield theory in the sense of Darden & Maull (1977), where the theories comprising the interfield are in turn reductively connected. In this context, it is crucial that the reduction postulates carry limited, context-free information, so that the theoretical context is lost while the reductive connection is made.
This circumstance allows us to argue that, while the individual theories make up the field, Nagelian reduction relationships between these individual theories do not in turn amount to tout court reduction of the field. As is the case in the reduction between chemistry and physics, Nagelian reduction thus allows theoretical independence of the field.
In the concept of naturalized reduction I have developed, theoretical concepts may be freely borrowed from other fields, and reused as theoretical ‘patches’ in the development of further theories. Such theoretical patching involves a loss of context. As an aside, the ‘loss of context’ that may accompany intertheory reduction may formally be specified in terms of the ‘chunk and permeate’ approach to theories developed for instance by Brown & Priest (2004, 2008). They hold that such (paraconsistent) ‘chunk and permeate’ structures are even present in individual theories. Alternatively, these concepts can also be logically developed as part of a semantic or structuralist model of theory nets and intertheoretic links. For now, we will forgo these formal specifications.
4.2 The unity of science: reducing theories and disciplinary autonomy
The last step in my naturalized approach is evaluating the reconstruction in terms of a naturalized Nagelian approach to the unity of science. Up to this point, I have argued that considering the absolute reaction rate theory as a case of naturalized Nagelian reduction has given us additional insight into the structure and nature of the intertheory relationship that applies in this case. We now turn to the last step of the naturalized approach, which is the classification of the case study in terms of either a reductive (or non-reductive) model.
The analysis of absolute reaction rate theory in terms of the naturalized Nagelian model has illuminated two unique features of the theory which are of further interest for the philosophy of science. These are:
- The specification of the transition state as a unique sort of molecule. This explicitly adds insights from the reduced theory to the reducing theory.
- The comparison of several potential reducing theories in terms of their explanatory strength, which gives additional mechanistic insight into the theory of chemical reaction rates.
A reductive model will in the final analysis attempt to map these features into the reducing theory. Such a ‘mapping’ is only possible after the explanation is complete: it is not possible to say a priori what the statistical mechanical or thermodynamic features of the transition state are before the explanation of the theory has been established, or to decide a priori which of the competing reducing theories is the best ‘fit’.
In terms of a reductive model, therefore, the reducing theories and the reduction postulates need to be read as a holistic whole. The specification of the transition state in terms of a ‘special’ kind of molecule illustrates that the reduction postulates in this case must be read as a case of representation in which the reducing theory introduces a specific notion deriving from the reduced theory into the reducing theory. The specification of the transition state in the present case cannot be read as a Nagelian case of identification or some form of extensional correlation if the conceptual patch made by the reduced theory is ignored.
Once this conceptual patch has been ‘imported’ into the reducing theory, the notion of the transition state stands in an analogy relationship to the Arrhenius condition. As we have seen, Dizadji-Bahmani et al. (2010) argue that the specialization, application, and transformation that characterize their version of Nagelian reduction yields a final theory that stands in such an analogy relation to the theory to be reduced. For the present case that implies that the precise specification of the transition state which is furnished by absolute reaction rate theory is analogous to Arrhenius’ ‘active’ form of cane sugar.
An important consequence of this conceptual patching of the reducing theory is that in the reduction the reduced theory cannot be eliminated: it retains its own status as a valid theory of a phenomenon.
The comparison (and to some degree competition) of several reducing theories is the second important feature of this particular test case. Specifically, the three formulations of the Eyring equation that are of interest are the collision theory, the thermodynamic formulation, and the statistical mechanical formulation. All of these three theories remain valid in the explanation. In this way, comparison of the various approaches is used to illuminate various aspects of the mechanisms of chemical reactions.
It is harder to read this second feature as one that is inherent even in a liberal reading of Nagel’s model, even though it does provide clues as to how one might go about evaluating the reductive strength of the three theories involved. The evaluation of such a reductive strength, combined with the associated theory survival, would form an interesting extension to Nagel’s model. Even while it seems possible to extend it in this particular way, it is interesting at this point to investigate whether non-reductive theories provide us with an avenue to accommodate this feature more naturally.
Darden and Maull’s concept of ‘interfield theories’ (or Harris’ interdisciplinarity) as an approach to the explication of absolute reaction rate theory are certainly promising in this regard. Absolute reaction rate theory fits with the idea of an interfield theory in the sense that it provides new connections between not only chemistry and statistical mechanics, but also between candidate reducing theories from different fields such as thermodynamics. Similarly, the theory necessarily draws on concepts from chemistry, physics, and thermodynamics to provide its overall explanation, since the insights offered by the absolute theory depend in significant measure upon the comparisons between the different ‘reducing’ candidate theories.
The fulfillment of the remainder of Darden and Maull’s criteria seems a bit more problematic, in the sense that the theory does not refocus our attention on ‘previously neglected items or domains’ or predicts new such items or domains. The theory is open to further concretization, and has to some degree initiated new areas of research. Having said that, the first two criteria seem to be the key criteria that allow us to classify the theory as an ‘interfield’ theory, so that Darden and Maull’s model is at least partially successful. However, while the case at hand fits some of the criteria for such an ‘interfield’ theory or ‘interdisciplinary entity’, it leaves the issue of reduction somewhat unsatisfactorily unresolved.
Darden and Maull’s notion of interfield theories is usually advertised as a non-reductive theory, and its use seems to prompt us to come up with a new model for the unity of science. It can be argued, however, that their model of ‘interfield’ theories is reductionist in the sense that it ascribes to some sort of derivation or explanation and at the same time liberalizes Nagel’s reduction postulates to include constitutive theories. This seems to me a defensible classification to the extent that Darden and Maull seem to have an issue with reductionism and elimination rather than reduction as a more liberal theory of explanation.
The Neurathian model, like that of Bokulich, is based on structural relationships between the various constituting theories. Such structural relationships do exist, as we have already argued, between the notion of the transition state and the ‘active’ form of cane sugar studied by Arrhenius. They also exist between the three competing theories: the form of the mathematical equations for the reaction rate constant is similar.
None of the ‘non-reductive’ models, moreover, are incompatible with the view of the network of intertheory relations we have sketched in Figure 3, where Nagelian connections exist between the different theories that form the network, and where the overall reduction is specified in terms of this network. Therefore at this stage there seem to be no good reasons to conclude that a Nagelian model cannot fruitfully deal with the complexities of theory comparison in the present case.
5. Conclusion: the unity of chemistry and physics
Naturalized Nagelian reduction has yielded interesting perspectives on the case of absolute reaction rate theory. My aim in this conclusion will be to gather up some of the gains and suggest avenues for further work.
The heuristic approach to Nagelian reduction followed in this paper has suggested that the two salient features of absolute reaction rate theory – the specification of the transition state and the ‘explanation by comparison’ through the various reducing theories – necessitate a realignment of Nagel’s model of reduction along the lines suggested by Klein (2009) and Dizadji-Bahmani et al. (2010), and more formal work to extend this model to the notion of a theory network.
The ‘explanation by comparison’ feature of absolute reaction rate theory also suggests interesting additional formal work in the philosophy of science, in which several candidate reducing theories can be evaluated on their explanatory strength. A feature of such a (future) formal development will have to be that it accounts for the insights offered by the various candidates for the reducing theories. It also needs to clarify why these candidates are not eliminated.
As the current example suggests, the unity of science is most properly conceived as a network of interlocking theories, which provide mutual support to each other. This seems at first sight more compatible with the various non-reductive theories we have discussed than with the Nagelian model. However, a large drawback of the non-reductive schemes is that they do not allow for further specification and evaluation of the consequences of this fact. The reductive model, even in places where strict Nagelian reduction fails, at this point appears to be the superior science of science.
References
Back, M.H. & Laidler, K.J.: 1967, Selected Readings in Chemical Kinetics, Oxford: Pergamon Press.
Bokulich, A.: 2008, Reexamining The Quantum-Classical Relation: Beyond Reductionism And Pluralism, Cambridge: Cambridge University Press.
Brown, B. & Priest, G.: 2004, ‘Chunk and Permeate, a Paraconsistent Inference Strategy. Part I: The Infinitesimal Calculus’, Journal of Philosophical Logic, 33 (4), 379-388.
Brown, B. & Priest, G.: 2008, ‘Chunk and Permeate II: Weak aggregation, permeation and old Quantum Theory’, talk at The Fourth World Congress of Paraconsistency, 13-18 July 2008, University of Melbourne.
Cartwright, N.; Cat, J.; Fleck, L. & Uebel, T.: 1996, Otto Neurath: Philosophy between science and politics, Cambridge: Cambridge University Press.
Causey, R.C.: 1977, Unity of Science, Dordrecht: Reidel.
Cohen, R.S. & Neurath, M. (eds.): 1983, Otto Neurath: Philosophical Papers 1913 – 1946, Dordrecht: Reidel.
Darden, L. & Maull, N.: 1977, ‘Interfield Theories’, Philosophy of Science, 44 (1), 43-64.
Dizadji-Bahmani, F.; Frigg, R. & Hartmann, S.: 2010, ‘Who’s Afraid of Nagelian Reduction?’, Erkenntnis, 73, 393-412.
Dupré, J.: 1993, The disorder of things: Metaphysical foundations of the Disunity of Science, Cambridge, MA: Harvard University Press.
Eyring, H.: 1935, ‘The Activated Complex in Chemical Reactions’, The Journal of Chemical Physics, 3 (2), 107-115.
Eyring, H.; Walter, J. & Kimball, G.E., 1944, Quantum Chemistry, New York: Wiley.
Fazekas, P.: 2009, ‘Reconsidering the Role of Bridge Laws In Inter-Theoretical Reductions’, Erkenntnis, 71, 303-322.
Glasstone, S.; Laidler, K.J. & Eyring, H.: 1941, The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena, New York: McGraw-Hill.
Harris, M.L.: 2008, ‘Chemical reductionism revisited: Lewis, Pauling and the physico-chemical nature of the chemical bond’, Studies in History and Philosophy of Science, 39 (1), 78-90.
Hendry, R.F.: 2010, ‘Ontological reduction and molecular structure’, History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics, 41 (2), 183-191.
Hettema, H.: 2012, Reducing Chemistry to Physics: Limits, Models, Consequences, PhD dissertation, University of Groningen (Createspace publishing platform).
Klein, C.: 2009, ‘Reduction Without Reductionism: A Defence Of Nagel On Connectability’, The Philosophical Quarterly, 59 (234), 39-53.
Labarca, M. & Lombardi, O.: 2010, ‘Why orbitals do not exist?’, Foundations of Chemistry, 12, 147-157.
Laidler, K.J. & King, M.C.: 1983 ‘Development of Transition-State Theory’, Journal of Physical Chemistry, 87 (15), 2657-2664.
LePoidevin, R.: 2005, ‘Missing Elements and Missing Premises: A Combinatorial Argument for the Reduction of Chemistry’, British Journal for the Philosophy of Science, 56, 117-134.
Lombardi, O. & Labarca, M.: 2005, ‘The Ontological Autonomy Of The Chemical World’, Foundations of Chemistry, 7, 125-148.
Miller, W.H.: 1998, ‘Quantum and Semiclassical Theory of Chemical Reaction Rates’, Faraday Discussions, 110, 1-21.
Nagel, E., 1961, The Structure of Science: problems in the logic of scientific explanation London: Routledge & Kegan Paul.
Needham, P.: 2010, ‘Nagel’s analysis of reduction: Comments in defense as well as critique’, Studies in History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics, 41 (2), 163-170.
Neurath, O.:1983a, ‘The Departmentalization of Unified Science’, in: R.S. Cohen & M. Neurath (eds.), Otto Neurath: Philosophical Papers 1913 – 1946, Dordrecht: Reidel, pp. 200-205.
Neurath, O.: 1983b, ‘The Unity of Science as a Task’, in: R.S. Cohen and M. Neurath (eds.), Otto Neurath: Philosophical Papers 1913 – 1946, Dordrecht: Reidel, pp. 115- 120.
Potochnik, A.: 2011, ‘A Neurathian Conception of the Unity of Science’, Erkenntnis, 74 (3), 305-319.
Scerri, E.R.: 1998, ‘Popper’s naturalized approach to the reduction of chemistry’, International Studies in the Philosophy of Science, 12, 33-44.
Scerri, E.R.: 2007, ‘The Ambiguity of Reduction’, Hyle: International Journal for Philosophy of Chemistry, 13 (2), 67-81.
Shapere, D.: 1977, ‘Scientific Theories and their Domains’, in: F. Suppe (ed.), The Structure of Scientific Theories, Urbana: University of Illinois Press, pp. 518-570.
Spector, M.: 1978, Concepts of Reduction in Physical Science, Philadelphia: Temple University Press.
van Riel, R.: 2011, ‘Nagelian Reduction beyond the Nagel Model’, Philosophy of Science, 78 (3), 353-375.
Wigner, E.: 1938, ‘The Transition State Method’, Transactions of the Faraday Society, 34, 29-41.
Hinne Hettema:
Department of Philosophy, The University of Auckland, Private Bag 92019, Auckland, New Zealand; hhet001@aucklanduni.ac.nz